OEF Cryptage RSA
--- Introduction ---
Ce module regroupe pour l'instant 6 exercices sur le système de
cryptologie RSA : création d'un système RSA, crypter/décripter un
message, cryptanalyse.
Création RSA
1
,
,
,
.
.
,
,
.
2
 .
.
.
.
3
, ,
?
Cryptage RSA
,
,
,
.
:
?
N-1.
Décrypt RSA
.
.
1.
, 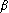 .
.
,
.
2.
, : ? N-1.
Cryptanalyse RSA
,
.
1.
,
.
,
.
2.
. : ? N-1.
Système de Diffie-Hellman
.
.
.
? ?
Système de Diffie-Hellman 0
.
mod .
?
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur le système de cryptage RSA. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, arithmetic, cryptology, informatics, RSA, factorization, modular_arithmetic,coding
 .
. 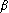 .
.