Un cours pour adultes qui veulent s'amuser un peu et repartir de zéro avec les statistiques.

Bienvenue

Ce cours parle de choses très simples, mais sur un mode à la fois "recherche" (on joue avec les notions, on veut que chacune d'entre elles ait une raison d'être qui soit satisfaisante) et à la fois "applications" (on n'étudie que des choses qui peuvent être utiles professionnellement).

Ce document n'est pas fini, mais s'il est utile à quelqu'un qui aimerait avoir la suite, il n'y a qu'à demander par mail...

Voici le menu des réjouissances :

Sommaire

• 0- Quelques bases
  • Écart
  • Proportion
  • Évolution
• 1- Indicateurs de position
  • Milieu
  • Moyenne
  • Médiane
  • Quel indicateur choisir ?
• 2- Indicateurs de dispersion

Dans le fil du texte, il y a tout un tas de petites questions. Essayez d'y répondre par vous même avant de regarder la solution. Pour y répondre, vous pouvez faire le calcul de tête ou alors avec un tableur (avec une calculatrice, c'est trop facile !).
Voici un lien vers un fichier tableur (avec 2-3 explications), si vous n'avez pas le vôtre sous la main.

Voici le même fichier à télécharger pour l'ouvrir dans votre tableur préféré (ce fichier est au format ".csv").

0- Quelques bases

En général, en statistique, on a au départ un ensemble de nombres et on veut en rendre compte de façon rapide et simple.

Par exemple, on a les salaires de tous les employés d'une entreprise et on veut résumer tout cet ensemble de nombres.
Il y a essentiellement deux choses à dire pour faire ce résumé :

• Autour de quelle valeur ces salaires se situent-ils ?
• Sont-ils proches les uns des autres, ou au contraire y a-t-il de fortes disparités ?

Les moyens de répondre à la première question s'appellent les résumés statistiques de position (voir la partie 1 de ce cours ). Ceux qui répondent à la seconde question sont les résumés statistiques de dispersion (voir la partie 2 de ce cours ).

Mais avant de parler de ces indicateurs, permettant de résumer un grand nombre de valeurs, voyons déjà ce qu'on peut dire quand on n'a que deux valeurs, mettons x₁ et x₂

Écart

Bon alors, on a deux salaires. On appelle x₁ le premier et x₂ l'autre. Pour apporter une réponse à la question 2 : sont-ils proches l'un de l'autre ?, il suffit de calculer l'écart entre les deux.
Tout le monde sait que cet écart se calcule grâce à une soustraction : x₂ - x₁
Si le nombre x₁ est inférieur au second, l'écart sera positif mais sinon, il sera négatif. Suivant les cas, cela peut avoir de l'importance ou pas. Mettons que, ici, ça a de l'importance...
On peut par exemple calculer l'écart entre 1000€ et 1500€ Réponse : 500€ ,
l'écart entre 1500€ et 1000€ Réponse : -500€ ,
l'écart entre 1501,69€ et 1502,37€ Réponse : 0, 68 € ,
l'écart de température entre -15°C et -17°C Réponse : -2°C ,
ou entre -8°C et +12°C Réponse : 20°C ou +20°C ,
l'écart d'âge entre 2 ans et 38 ans Réponse : 36 ans ,
ou encore entre 8 mois et 1 an Réponse : 4 mois ou ans (4 douzièmes). Comme , cet écart est an (un tiers d'année) .

Remarque : lorsque l'ordre dans lequel on considère les deux nombres n'a pas de signification particulière, le signe de l'écart n'a pas d'importance. Il peut être positif ou négatif suivant qu'on appelle x₁ la plus petite valeur ou la plus grande. Dans ce ca là, on ne mentionne pas le signe de l'écart : ça s'appelle l'écart en valeur absolue.

Proportion

Le problème c'est que, souvent, un écart donné seul n'a pas grande signification. Par exemple, 6 mois d'écart d'âge entre deux personnes, ce n'est pas grand chose pour des adultes mais c'est beaucoup pour des bébés. Pour être plus parlant, on utilise la notion de proportion.
Mathématiquement, c'est exprimé grâce à une fraction : 6 mois par rapport à 21 mois est noté . Comme (Pourquoi ? Réponse : car ), on voit que 6 mois par rapport à 21 mois, c'est exactement la même proportion que 2 mois par rapport à 7.

Bon. Les fractions, c'est super, mais beaucoup de gens n'y comprennent pas grand chose. Souvent, on leur préfère les pourcentages.
Ce sont des fractions par rapport à 100 : 12% est une notation pour désigner .
Combien de pour-cent représentent 6 mois par rapport à 21 ? Bonne question :-)
Pour le calculer, on utilise un calcul de proportionnalité. Suivant la façon dont vous l'avez appris à l'école, ce calcul peut être présenté différemment mais souvent les gens l'écrivent ainsi :

mois d'écart	6	?
par rapport à	21	100

Ce qui donne environ 28,6%.
On peut aussi se souvenir qu'une fraction, c'est somme une division, que (6 divisé par 21) égale environ 0,286 soit 28,6%.
Tout l'intérêt des pourcentages pour les calculs est ici : à partir de la valeur décimale obtenue en effectuant la division, il suffit de décaler deux fois la virgule pour obtenir le pourcentage.

Pouvez-vous calculer les proportions suivantes ?
Un salaire de 1000€ sur une masse salariale totale de 8000€ en fraction : , en valeur décimale : 0,125 , en pourcentage : 12, 5% .
Un salaire de 1 000 000 € sur une masse salariale totale de 1 008 000€ en fraction : ou, après réduction, , en valeur décimale : 0,99 , en pourcentage : 99% .
Une semaine pour un bébé âgé de 2 mois (combien de semaines compte un mois ? Réponse : dans un an de 12 mois, il y a 52 semaines, soit semaines par mois )
en fraction : 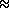(ou en comptant 4 semaines par mois...) , en valeur décimale : 0,116 (pour 4,3 semaine par mois) , en pourcentage : 12% (après avoir arrondi) .

Écart relatif, évolution

Pour revenir à nos deux valeurs précédentes, appelées x₁ et x₂ :
Quel est l'écart entre les deux ? Réponse : x₂-x₁. Cet écart est souvent appelé absolu (C'est un détail, mais ne confondons pas "écart absolu" et "écart en valeur absolue" : cet écart absolu peut être positif ou négatif, contrairement à l'écart en valeur absolue mentionné précédemment).
Quelle proportion cela représente-t-il par rapport à x₁ ? Réponse : (c'est à dire l'écart divisé par la première valeur). Ce dernier résultat est souvent exprimé en pourcentage mais peut aussi être donné en fraction ou en valeur décimale. C'est ce qu'on appelle l'écart relatif entre les deux valeurs.
Souvent, les deux valeurs correspondent à deux mesures successives dans le temps : par exemple, en 2015 je gagne 1500€ par mois et en 2016 je vais gagner 2500€ par mois. Quelle augmentation absolue cela représente-t-il ? Une augmentation de 1000€. Quelle augmentation relative cela représente-t-il ? Une augmentation de soit environ +67%

L'écart relatif est donc souvent utilisé dans un contexte d'augmentation ou de diminution : il est dans ce cas appelé pourcentage d'évolution.

Deux enfants sont âgés de 5 et 8 ans.
Quel est l'écart d'âge relatif par rapport au plus jeune ? En pourcentage : 60% .
Quel est l'écart d'âge relatif par rapport au plus âgé ? En pourcentage : 37, 5% .
Un prix augmente de 10€ à 15€. Quel pourcentage d'augmentation cela représente-t-il ? En pourcentage : 50% .
Un prix baisse de 15€ à 10€. Quel pourcentage de diminution cela représente-t-il ? En pourcentage : -33% .

Comme on le voit sur ces exemples, si on calcule un écart relatif par rapport à la première valeur x₁ on n'obtient pas le même résultat que si on le calcule par rapport à l'autre valeur.
Conventionnellement, on exprime toujours l'écart relatif par rapport à la première valeur.
Cela donne lieu à tout un tas d'erreurs : par exemple, si on a dans un sens une évolution de +50%, on n'a pas dans l'autre sens une évolution de -50%, mais de -33%...
Si on augmente deux fois de 20%, l'augmentation globale n'est pas de 40%, etc.
En bref : attention en additionnant ou soustrayant des pourcentages. S'il s'agit d'écart relatif ou d'évolution ces calculs avec les pourcentages sont faux.

Conclusion :

On s'est intéressé à deux valeurs et à la mesure de leur écart, c'est à dire de leur dispersion. On peut broder encore longtemps là-dessus, mais par rapport à l'ambition initiale de ce cours, on n'a pas fait grand chose.
Il faudrait maintenant s'intéresser à la position, c'est à dire : si on devait résumer nos deux valeurs par une seule (autour de laquelle les deux valeurs vont se situer), comment peut-on procéder ? Les indicateurs statistiques de position (pour deux valeurs et aussi pour plus de deux !) sont l'objet de la page suivante .

Sommaire

• 0- Quelques bases
  • Écart
  • Proportion
  • Évolution
• 1- Indicateurs de position
  • Milieu
  • Moyenne
  • Médiane
  • Quel indicateur choisir ?
• 2- Indicateurs de dispersion

1- Indicateurs de position

Résumé de l'épisode précédent :
En statistique, on a en général de grandes séries de nombres qu'on cherche à résumer par des indicateurs.
Il y a des indicateurs de position, qui servent à avoir une idée de "autour de quelle valeur se situent les nombres qu'on étudie".
Il y a des indicateurs de dispersion, qui servent à avoir une idée de "si les nombres étudiés sont proches les uns des autres ou pas".

Milieu

Comme auparavant, on commence par se demander ce qui se passe quand on a seulement deux valeurs : x₁ et x₂. Si on veut savoir "autour de combien ces deux valeurs se situent, il suffit de calculer la valeur qui est "au milieu entre x₁ et x₂". Par exemple, si x₁=50€ et x₂=100€, quelle est la valeur au milieu entre ces deux valeurs ? C'est 75€...

Comment calculer ce milieu ? Réponse : en calculant
On peut par exemple calculer le milieu entre 1000€ et 1500€ Réponse : 1250€ ,
le milieu entre les températures -15°C et -17°C Réponse : -16°C (bien sûr) ,
ou entre -8°C et +12°C Réponse : 2°C ,
le milieu entre 1501,69€ et 1502,37€ Réponse : 1502, 03€ ,
ou encore entre 8 mois et 1 an Réponse : 10 mois. .

Moyenne

Voyons maintenant ce qui se passe lorsqu'on a plus de deux valeurs.
Par exemple, trois :-)
Notons-les x₁, x₂ et x₃. Supposons en outre qu'elles sont rangées par ordre croissant, c'est à dire de la plus petite à la plus grande, c'est à dire que .
On a alors le choix : soit on considère que la valeur "du milieu" est x₂ : on utilise alors ce qui en statistique s'appelle la médiane (voir après) ;
soit on calcule la moyenne de x₁, x₂ et x₃.
On utilise alors la formule :
La moyenne est le nombre tel que si on additionne x₁, x₂ et x₃, on obtient la même somme qu'en additionnant 3 fois la moyenne : si les trois nombres x₁, x₂ et x₃ étaient égaux, mais que leur somme restait inchangée, quelle devrait être leur valeur ? Réponse : cela devrait être leur moyenne.

La définition de la moyenne est donc assez abstraite, comme on vient de le constater. Cependant, on rencontre souvent des moyennes dans la vie courante, c'est pourquoi nous y sommes habitués.
Dans le cas où il y a plus que trois valeurs, la façon de calculer la moyenne est la même : on additionne tout et on divise par le nombre de valeurs.
Parfois, on affecte chaque valeur d'un coefficient, permettant de donner plus ou moins d'importance à la valeur. Le calcul de la moyenne est alors le suivant :
Multiplier chaque valeur par son coefficient, tout additionner : on obtient une première somme. Additionner tous les coefficients. Diviser la première somme par la somme des coefficients.

Voilà quelques exemples. Essayez de retrouver chaque moyenne. Si vous n'y arrivez pas, il y a des indications pour vous aider.

nom	Joe	Jack	Wiliam	Averell
taille	1.2	1.6	1.7	2

moyenne des tailles : 1.625 tout ajouter et diviser par 4...

taille	1.2	1.3	1.4	1.5
effectif	2	3	5	1

taille moyenne : 1.35 (arrondie au centième, c'est à dire avec deux chiffres après la virgule). La taille 1.2 doit être comptée deux fois, puisqu'ils sont deux à avoir cette taille ... A la fin, il faut diviser par 11...

valeur	1200	1500	1700	2200
coefficient	0.1	0.4	0.3	0.1

valeur moyenne : 1611 (arrondie à l'unité) multiplier chaque valeur par son coefficient... à la fin, diviser par la somme des coefficients, soit ici 0.9

Médiane

Si on reprend le cas où il y a trois valeurs, par exemple 2.3 ; 1.4 et 5.0, alors on peut bien sûr calculer leur moyenne pour obtenir un indicateur de position. Mais on peut aussi calculer leur médiane.
Ici, la médiane est 2.3. En effet, si je classe les valeurs dans l'ordre, celle du milieu est 2.3. Il y en a une qui est inférieure à cette valeur et une qui est supérieure.

Un autre exemple : on ajoute la valeur 1.1 à la liste précédente. Les 4 valeurs sont 1.1 ; 2.3 ; 1.4 et 5.0. Quelle est la médiane ? Si on classe les valeurs dans l'ordre, on obtient . Bien sûr, le problème est alors qu'il n'y a aucune valeur centrale : il y a le groupe des deux valeurs les plus petites, celui des deux valeurs les plus grandes, et rien entre les deux groupes. Dans ce cas, la médiane peut être n'importe quelle valeur située entre les deux groupes, c'est à dire entre 1.4 et 2.3. En général, pour fixer les choses, on prend pour médiane le milieu entre 1.4 et 2.3, soit ici 1.85 (pourquoi ?)

Plus généralement, pour obtenir la médiane d'une série de valeurs, on les classe et on essaye de les partager en deux groupes de même effectif : celui des plus petites valeurs et celui des plus grandes.
Si l'effectif total est impair, la médiane est la valeur restée "toute seule au milieu".
Si l'effectif total est pair, la médiane est le milieu entre la dernière valeur du premier groupe et la première du second groupe.

Pouvez-vous trouver la médiane dans les trois cas suivants ?

nom	Joe	Jack	Wiliam	Averell
taille	1.2	1.6	1.7	2

taille médiane : 1.65

taille	1.2	1.3	1.4	1.5
effectif	2	3	5	1

taille médiane : 1.4 Il y a 11 valeurs ! La médiane est la 6ème... Les 11 valeurs sont : 1.2 - 1.2 - 1.3 - 1.3 - 1.3 - 1.4 - 1.4 - 1.4 - 1.4 - 1.4 - 1.5

taille	1.2	1.3	1.4
effectif	2	3	5

taille médiane : 1.35 Il y a 10 valeurs ! La médiane est au milieu entre la 5ème et la 6ème... Les 10 valeurs sont : 1.2 - 1.2 - 1.3 - 1.3 - 1.3 - 1.4 - 1.4 - 1.4 - 1.4 - 1.4

Quel indicateur choisir ?

...à faire...

---

• 0- Quelques bases
  • Écart
  • Proportion
  • Évolution
• 1- Indicateurs de position
  • Milieu
  • Moyenne
  • Médiane
  • Quel indicateur choisir ?
• 2- Indicateurs de dispersion