Déterminant
Guide
Le texte suivant introduit les déterminants en en donnant une construction puis donne quelques propriétés. On espère compléter ultérieurement la partie déterminant et systèmes linéaires.- Déterminant des matrices
- Déterminant et vecteurs
- Déterminant d'un endomorphisme
- Déterminant et systèmes linéaires
Déterminant des matrices
- Définition de l'application déterminant
- Conséquences immédiates de la définition
- Petits cas
- Développement par rapport à une colonne
- Démonstration de l'existence et de l'unicité
- Matrice triangulaire
- Matrice inversible et déterminant
- Multiplicativité
- Transposition
- Exercices
Définition de l'application déterminant
Soit Mn,m(K) l'ensemble des matrices à coefficients dans un corps K (égal à ou ) ayant n lignes et m colonnes, Mn(K) l'ensemble des matrices carrées d'ordre n à coefficients dans K. On note- In la matrice identité d'ordre n
- A = ((ai j)) où i est l'indice des lignes et j l'indice des colonnes
- A1, ..., An ses n colonnes : A=(A1, ..., An).
Théorème
Il existe une unique application
,
appelée déterminant vérifiant les propriétés suivantes
La propriété
(D2) est vraie même si les colonnes
ne sont pas à côté l'une de l'autre, nous le démontrons à partir des propriétés
telles qu'elles ont été énoncés ici :
-
(D1) pour tout
j=1,..., n, pour
tous
a et
b appartenant à
K,
pour
A1,..., An et
Bj des vecteurs colonnes,
+ .
- (D2) s'il existe un indice j tel que , .
- (D3) .
(D'2) s'il existe des indices
j et
k tels que
,
.
Conséquences immédiates de la définition
- S'il existe deux indices
j et
k différents tels que
Aj = Ak = B, .Si deux colonnes sont égales ou proportionnelles, le déterminant est nul.DémonstrationEn échangeant successivement la i-ième colonne avec sa voisine de manière à l'amener à la place j-1, on se retrouve dans le cas où les deux colonnes égales sont côte à côte (d'après la propriété précédente, le signe a peut-être changé).
- si
,
.
- si
.
- Si
où B est mis à la place de la m-ième colonne.
Démonstration= = +...+
+...+d'après (D1)=d'après (D2)=
Petits cas
Pour n=1, on a nécessairement .Pour n=2, on a nécessairement
det
= det
=
det
+
det
=
a det
+ c det
=
a ( det
+
det
)
+ c (det
+det
)
=
a ( 0 + d) det
+
c (
b det
+ 0)
=
a d -b c
Développement par rapport à une colonne
Lemme
Soit
Ai j la matrice extraite de
A obtenue en enlevant
la
i-ième ligne et la
j-ième colonne. Alors,
Idée de la démonstration
.
Faisons la démonstration pour le développement par rapport à la première colonne.
On écrit
avec
Ei le vecteur colonne formé de
0 sauf à la
i-ième ligne
où il y a
1. On a grâce à
(D1)
Regardons le terme
où
est la colonne
Ak où on remplace le
i-ième élément par
0.
On remarque alors que l'application qui à une matrice
B d'ordre
n-1 associe
avec
la matrice colonne obtenue à partir de
B en rajoutant un
0
à la place
i, vérifie les deux premières propriétés du déterminant
et vaut
sur l'identité
In-1. Donc
.
Par exemple,
ici
i = 1
En faisant des manipulations sur les colonnes du type
remplacer
Ak par
Ak - ai k Ei, on obtient que Exemple
.
Exemple
Dans l'exemple ci-dessous, par rapport à quelle colonne a-t-on développé ?
Démonstration de l'existence et de l'unicité
Supposons par récurrence que l'existence et l'unicité de sont démontrés sur Mn-1(K) avec n>1. La fonction déterminant sur Mn-1(K) est notée en vert : .Suposons l'existence de sur Mn(K) et montrons son unicité.
-
Fixons deux entiers
i et
j. À une matrice
B=(bi j) de
Mn-1(K),
on attache la matrice
B(i,j) obtenue en rajoutant une colonne à la place
i et une ligne à la place
j formées de 0
sauf à leur intersection où l'on met 1 :
Par exemple :La fonction satisfait toutes les propriétés pour le déterminant sur Mn-1(K) et lui est donc égale : pour D1 et (D2), faites-le ! le signe garantit la condition pour (D3), car d'après (D1), si on part de la matrice Id(i,j), après échanges de colonnes voisines, le coefficient 1 arrive sur la diagonale et le signe est devenu 1.Le faire par exemple pourId(5,4)=
- Par (D1) et (D3) (voir conséquences immédiates ), ne change pas si on met n'importe quel coefficient à la i-ième ligne hors la j-ième colonne.
-
Si la fonction
existe pour
Mn,n(K), on trouve par
(D1) la formule pour tout
indice de ligne
i entre
1 et
n :
.où Ai j est la matrice extraite, c'est-à-dire la matrice A privée de sa i-ième ligne et de sa j-ième colonne. Le membre de droite est fait avec des déterminants d'ordre n-1 dont on sait qu'ils existent et sont uniques par hypothèse de récurrence. Cela démontre l'unicité de sur Mn,n(K).
Démontrons l'existence de sur Mn(K).
Définissons une fonction sur
Mn(K) provisoirement appelée
par la formule
(développement par rapport à la
i-ième ligne) :
Elle vérifie (D2) : justification
Elle vérifie (D3) : justification
L'unicité prouve de plus que les fonctions ainsi définies sont tous égales.
pour
i = 2 :
Elle vérifie
(D1) :
justification
=
+
+
Soit
k l'indice de la colonne où l'on a remplacé
Ak par
a Ak+ b Bk et
la matrice extraite correspondant à la matrice
(A1,...,Bk,...An). Dans la somme définissant
,
aik est remplacé par
aik+bik et
Ai k ne change pas ; par contre
pour
j différent de
k,
ai j ne change pas et
est remplacé par
en utilisant la propriété
(D1) pour
.
Elle vérifie (D2) : justification
Soit l'indice
k tel que les colonnes d'indice
k et d'indice
k+1 soient égales.
Les matrices extraites
Ai j intervenant dans la formule
ont toutes deux colonnes égales et sont donc nulles
sauf les matrices extraites
Ai k et
Ai k+1 qui sont égales :
.
Elle vérifie (D3) : justification
L'unicité prouve de plus que les fonctions ainsi définies sont tous égales.
Matrice triangulaire
Théorème
Si
A est une matrice triangulaire inférieure, le déterminant de
A
est le produit de ses coefficients diagonaux
ai i : on a
Démonstration
.
On raisonne par récurrence. On développe par rapport à
la première colonne si la matrice est triangulaire supérieure et par
rapport à la dernière colonne si la matrice est triangulaire inférieure.
Exemple
Le déterminant de
est égal à fois le déterminant de





.
Par récurrence, il vaut





Matrice inversible et déterminant
Théorème
Le déterminant
d'une matrice carrée
A d'ordre
n est nul si et seulement si le
rang de
A est strictement inférieur à
n, c'est-à-dire si et
seulement si
A n'est pas inversible.
Démonstration :
- Si rg A < n, un des vecteurs-colonne de A est combinaison linéaire des n-1 autres. Donc .
- Si rg A = n, alors A est inversible, on se ramène par des manipulations de colonnes (par la méthode des pivots) à une matrice triangulaire dont les éléments diagonaux sont tous non nuls. A chaque transformation, le déterminant est multiplié par un scalaire non nul. Donc, .
Ainsi,
Théorème
Pour que
n
vecteurs d'un espace vectoriel de dimension
n forment une base, il
faut et il suffit que le déterminant de la matrice formée avec leurs
composantes dans une base quelconque soit non nul.
La valeur absolue du déterminant d'une base a une interprétation géométrique si l'on utilise le produit scalaire naturels de l'espace vectoriel comme volume du parallépipède construit à partir de la base.
Multiplicativité
Théorème
Si
A et
B sont deux matrices carrées d'ordre
n;
Démonstration :
.
En particulier, si
A est inversible,
Si
B n'est pas inversible,
A B ne l'est pas non plus et on a bien
0 = 0.
Si
B est inversible,
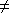 0. L'application
vérifie
toutes les propriétés du théorème-définition (exercice).
Par unicité, on a donc
0. L'application
vérifie
toutes les propriétés du théorème-définition (exercice).
Par unicité, on a donc
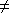 0. L'application
0. L'application
F : Mn(K)  K
K
définie par
 K
K
.
Transposition
Théorème
Si
At est la
transposée
On peut ainsi développer le déterminant par rapport à une ligne et les propriétés du
théorème-définition restent vraies si on remplace les colonnes par les lignes.
La transposée de la matrice
((ai j)) est la matrice
((aj i)).
Par exemple, la transposée de
est la matrice
.
de la matrice
A,
.
Exercices
Exercices
- Des questions auxquelles il faut répondre très vite
- Applications des règles de multilinéarité
- Applications des règles de permutation
- Applications de la multiplicativité
- Produit
- Calcul de déterminant I
- Calcul de déterminant II
- Calcul de déterminant "à la Gauss"
- Déterminant paramétré
- Déterminant paramétré
- Déterminant et rang
Déterminant et vecteurs
- Déterminant et vecteurs
- Produit mixte
- Produit vectoriel
- Produit vectoriel : propriétés
- Aire et déterminant
Déterminant et vecteurs
Soit E un espace vectoriel de dimension n et une base.Définition :
Soit
(v1, ... , vn)
n vecteurs. On appelle déterminant de
(v1, ... vn) dans la base
le déterminant
de la matrice des composantes des
vi dans la base
.
On le note
.
Proposition
Le déterminant de
n vecteurs dans une base dépend de la base :
Si est une autre base, si P est la matrice de passage de à , on a
Si est une autre base, si P est la matrice de passage de à , on a
Produit mixte
Considérons un espace vectoriel E de dimension n muni d'un produit scalaire. Choisissons une base orthonormée.
Soit muni du produit scalaire où v = (xi), v' = (x1',...,xn'). Dans ce cas, la base canonique (e1,...,en) est orthonormée, c'est-à-dire vérifie si i=j et 0 sinon.
Théorème
Le déterminant de la matrice de passage
d'une base orthonormée à une autre base orthonormée
est égale à  1 .
1 .
 1 .
1 .
Démonstration
La matrice de passage
P
vérifie
P Pt = Id. Donc on a
.
Une fois choisie une base orthonormée
,
le déterminant sépare les bases orthonormées en deux sous-ensembles :
- celles telles que le déterminant de la matrice de passage de est égal à 1 (on les appelle base orthonormée directe)
- celles dont le déterminant de la matrice de passage de est égale à -1 (on les appelle base orthonormée indirecte).
Définition
Soit
E un espace vectoriel
de dimension
n muni d'un produit scalaire (euclidien) et d'une base orthonormée
de référence.
On appelle produit mixte de
n vecteurs
v1,..., vn (on note aussi
(v1,..., vn)) le déterminant de
v1,..., vn dans la base
ou ce qui revient au même dans toute base orthonormée directe.
Produit vectoriel
Soit un espace vectoriel E de dimension n muni d'un produit scalaire et d'une base orthonormée .Définition : Soit
n-1 vecteurs
v1,..., vn-1.
On appelle produit vectoriel de
v1,..., vn-1 l'unique vecteur
noté
tel que
Un tel vecteur existe grâce au théorème suivant :
pour tout vecteur w de E.
Théorème
Soit un espace vectoriel
E de dimension
n muni d'un produit scalaire.
Soit
f une forme linéaire de
E dans
. Alors,
il existe une unique vecteur
a dans
E tel que
.
Exemple : Prenons
n=2 :
le produit vectoriel de
v est le vecteur déduit de
v par une rotation
d'angle
: on doit en effet avoir
.
Si les composantes de
v,
w et
dans la base
sont respectivement
(a, b),
(x,y) et
(c,d), on doit avoir
a y - b x = c x + d y pour tous
x et
y dans
K.
Donc les composantes de
sont
(-b, a).
Produit vectoriel : propriétés
Les propriétés suivantes se déduisent de la définition et des propriétés du déterminant :-
Soit
i un entier entre 1 et
n-1. L'application
est linéaire :
-
- est perpendiculaire à chacun des vecteurs vj
- Le calcul des composantes du produit vectoriel de deux vecteurs en dimension 3 est une conséquence de la formule de développement par rapport à la dernière colonne : Si w est de composantes (w1,..., wn) dans la base et si A est la matrice des vecteurs colonnes de v1,...v(n-1) dans la base , on a où la matrice obtenue à partir de A en enlevant la i-ième ligne.
- Si les vecteurs
sont linéairement indépendants,
est non nul et la famille de vecteurs
forment une base directe : le déterminant de ces vecteurs dans la base est strictement positif .
Exercice : Retrouver toutes les propriétés du produit vectoriel que vous connaissez
en dimension 3 comme conséquences des propriétés du déterminant.
Aire et déterminant
Théorème
Dans le plan, l'aire
du parallélogramme formé à partir des
vecteurs
v1 et
v2 est égale à la valeur absolue du déterminant
de
v1 et
v2
Démonstration
L'aire du parallélogramme construit sur les deux vecteurs
(a,b) et
(c,d)
est égale à
: calculons l'aire de la moitié de ce parallélogramme qui
est un triangle
T.
Rappelons que l'aire d'un triangle ne change pas lorsqu'un des sommets se déplace
sur une parallèle au côté opposé :
Il ne reste plus qu'à découper le triangle T en trois triangles et à déformer chacun d'entre eux sans en changer l'aire jusqu'à obtenir une figure remplissant la moitié d'un rectangle de côtés de longueur a et b (et donc d'aire a b) auquel on a enlevé un rectangle de côtés de longueur c et d donc d'aire c d. Magique !
Théorème
L'aire du parallélogramme formé à partir des
vecteurs
v1 et
v2 est égale à la norme du produit
vectoriel de
v1 et de
v2.
Démonstration
:
Plaçons-nous dans le plan contenant les deux vecteurs
v1 et
v2.
L'aire
A à calculer est égale au produit de la longueur
du vecteur
v1
et de la longueur
h de la hauteur
correspondante. Le vecteur
w associé à cette hauteur
est la projection de
v2 sur la droite perpendiculaire à
v1.
Si
w1 = (-b,a) est le vecteur normal à
v1 = (a,b) de même norme, on a donc
Théorème
Le volume du parallélépipède formé à partir des
vecteurs
v1,
v2 et
v3 de
est égal à la valeur absolue du déterminant de
v1 et de
v2 et
v3 calculée dans une base orthonormée.
Démonstration :
Le volume
V est égal au produit de l'aire
A du parallélogramme formé
par les vecteurs
v1 et
v2 et de la longueur
H de la hauteur du parallélépipède
correspondante. Cette hauteur est par définition perpendiculaire au plan engendré par les vecteurs
v1 et
v2. Si
w est le vecteur représentant cette hauteur, il est donc
colinéaire à
et c'est la projection du vecteur
v3 sur la droite engendrée par
.
Ainsi, on a
A =
Déterminant d'un endomorphisme
Soit E un espace vectoriel de dimension finie n et f un endomorphisme de E. Si .Définition
Le scalaire
ne dépend
pas de la base
.
On l'appelle le déterminant de
f.
On applique la formule de changement de base : si P est la matrice de passage de la base à une base Par multiplicativité du déterminant,
Théorème
-
-
-
f est un automorphisme de
E si et seulement si
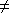 0
et on a alors
0
et on a alors
Déterminant et systèmes linéaires
Soit un système linéaire AX = B à n inconnues et n équations. La matrice A est donc une matrice carrée d'ordre n.Définition :
Si
est non nul, le système est appelé système de Cramer.
Théorème
Un système de Cramer
AX = B
admet une solution unique donnée par les formules
avec Bj la matrice obtenue à partie de A en remplaçant la j-ième colonne par la colonne B.
Démonstration :
Le système linéaire peut s'écrire en introduisant les colonnes
de
A :
et on peut utiliser alors la formule
Exemple :
Si
ad - bc 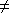 0, le système
0, le système
On utilise aussi les déterminants dans le cas de systèmes linéaires qui ne sont
pas de Cramer.
 0, le système
0, le système
a une unique solution donnée par
x = y =