Droites remarquables, transformations

Sommaire

Ce document rédigé pour les étudiants de la licence scientifique générale (L3 pour des futurs professeurs des écoles à l'université Paris-Sud) accompagne une partie du cours de géométrie basé sur l'ouvrage de Daniel Perrin : Mathématiques d'école : nombres, mesures et géométrie publié par Editions Cassini (402 p. ISBN 978-2-84225-158-1) . On y fait référence par ME.

ME exercice 187, 185 renvoie à l'exercice 187 de la nouvelle édition, 185 de la première. De même pour les pages ou les propositions.
ME VI.1. renvoie à la partie 1 du chapitre 6.

Son but est d'illustrer les révisions du chapitre IV de ME en liant transformations et droites remarquables du triangle. Les premières constructions à la règle et au compas sont établies [ME.VI].

Préliminaires

Droites remarquables du triangle et transformations

  1. Symétrie orthogonale et Médiatrice d'un segment
  2. Homothétie , Théorème de Thalès et Médianes
  3. Hauteurs
  4. Bissectrice d'un secteur angulaire, d'un angle
  5. Bissectrices dans un triangle

Applications

Cas d'isométrie

Si deux triangles sont isométriques (c'est-à-dire s'il existe une isométrie qui envoie l'un sur l'autre), alors leurs angles et leurs côtés homologues sont égaux. On obtient donc 6 égalités. Pour montrer que deux triangles sont isométriques, il suffit de 3 égalités bien choisies. On rappelle ici les trois cas d'isométrie pour les triangles quelconques (pour des énoncés plus précis, voir [ME.IV.4.a]) et on illustre le premier à l'aide de figures mobiles.

Pour une application des cas d'isométrie, voir la démonstration du théorème - définition des polygones convexes réguliers.

Premier cas d'isométrie

Premier cas : Si deux triangles ont un angle égal compris entre deux côtés égaux alors ils sont isométriques.
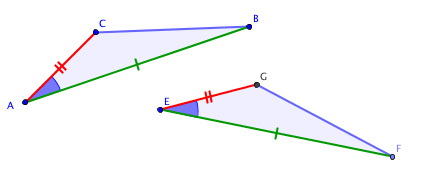
figure premier cas

Remarque : Il est essentiel que l'angle égal soit compris entre les deux côtés égaux. Il suffit de regarder cette figure .
Mais ce n'est pas utile pour les triangles rectangles .

Figures mobiles :

Contre-exemple

Les triangles ABC et ABC' ont un angle égal et deux côtés égaux mais ils ne sont pas isométriques ; l'aire de ABC est strictement plus petite que celle de ABC'

figure contre exemple

Les deux triangles sont directement isométriques.

Sur la figure, on voit comment les hypothèses permettent de superposer peu à peu le triangle A B C sur le triangle E F G. On commence par translater A B C pour amener A sur E, puis on fait tourner le triangle autour de E pour superposer B sur F. Alors C est amené en G. Les triangles sont directement isométriques.

Les deux triangles sont indirectement isométriques.

Sur la figure, on voit comment les hypothèses permettent de superposer peu à peu le triangle A B C sur le triangle E F G. On commence par translater A B C pour amener A sur E, puis on fait tourner le triangle autour de E pour superposer B sur F. Ensuite on retourne le triangle selon (E F) (symétrie d'axe (E F)). Les triangles sont indirectement isométriques.

Deuxième cas d'isométrie

Deuxième cas : Si deux triangles ont deux angles égaux et un côté égal, alors ils sont isométriques.
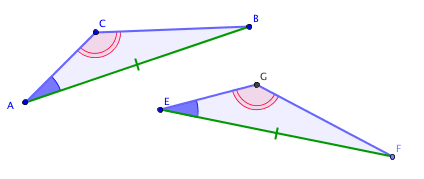
figure deuxième cas

Remarque : Si deux triangles ont deux angles égaux, leurs trois angles sont égaux.

Troisième cas d'isométrie

Troisième cas : Si deux triangles ont leurs trois côtés égaux alors ils sont isométriques.
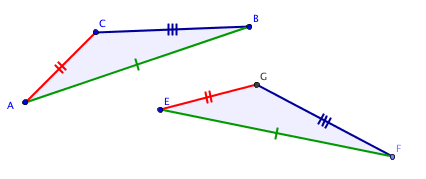
figure troisième cas

Remarque : Ce cas est très utile pour construire, à l'aide d'un compas, un triangle isométrique à un triangle donné, par exemple, pour reporter un angle.

Cas d'isométrie des triangles rectangles

Cas d'isométrie des triangles rectangles : Si deux triangles rectangles ont deux côtés homologues égaux, alors ils sont isométriques.

Les hypoténuses sont des côtés homologues, les côtés de l'angle droit sont homologues.

Constructions à la règle et au compas (principe)

Ce chapitre comporte un contexte historique et culturel important, lire [ME. VI. Introduction].

Ici sont repris les principes de la construction à la règle et au compas, tels qu'ils sont posés dans [ME.VI.1.A]. Les constructions fondamentales sont établies au moment où les résultats nécessaires sont énoncés.

Soit un ensemble de n points du plan. On appelle figures constructibles à la règle et au compas à partir de :

Définitions : Point constructible à la règle et au compas à partir de .
  1. On dit qu'un point M est constructible à la règle et au compas en un pas à partir de s'il est l'intersection de deux figures constructibles à la règle et au compas à partir de calP .
  2. On dit qu'un point M est constructible à partir de si on peut le construit en un nombre fini de pas à partir de c’est-à-dire, précisément, s’il existe des points M1, M2,... , Mr tels que Mr = M et que, pour i = 1, ... , r - 1, est constructible en un pas à partir de .
  3. On dit alors que la construction est faite en r pas.

Comment rédiger un exercice de construction ?

Les deux premières parties ne sont pas le lieu de décrire la construction.

  1. La partie analyse détermine des conditions nécessaires vérifiées par les points à construire. Evidemment pour permettre l'analyse, une figure est nécessaire, on peut tricher pour la faire.
  2. Dans les exercices assez simples, les conditions déterminées par l'analyse sont suffisantes, c'est-à-dire nous assurent que les points ainsi construits répondent au problème. Dans un exercice plus complexe, il faut s'assurer que les points construits satisfont les propriétés demandées. C'est la partie synthèse.
  3. La partie construction est la description précise (mais sans justification) des étapes nécessaires au tracé de la figure. Il peut arriver que la construction ne suive pas le fil de l'analyse. On peut préciser le nombre de pas si cela est demandé ou pour comparer deux constructions.

Parallélogramme

Propriétés caractéristiques du parallélogramme

Soit A B C D un quadrilatère convexe (voir [ME. fig. 20 page 156, fig.5 page 152]). On dit que A B C D est un parallélogramme s'il vérifie l'une des propriétés équivalentes suivantes.

  1. Les côtés opposés sont parallèles.
  2. Les côtés opposés sont de même longueur.
  3. Les côtés [A B] et [D C] sont parallèles et de même longueur.
  4. Les côtés [A D] et [B C] sont parallèles et de même longueur.
  5. Les diagonales [A C] et [B D] se coupent en leur milieu.
  9. Les angles opposés sont égaux.
 figure

Constructions et parallélogramme

  1. Construction d'un parallélogramme : Les points A, B et D étant donnés, on utilise la propriété 5 pour construire le parallélogramme A B C D [ME. VI.1. e].
  2. De la construction du parallélogramme, on déduit la construction d'une parallèle à une droite donnée passant par un point donné grâce à la propriété 1 [ME.VI.1. e]. Dans la deuxième édition, on trouve une autre construction d'une parallèle .
  3. De la construction du parallélogramme, on déduit le report de longueur grâce à la propriété 2 [ME. VI.1.f].

Démonstrations à l'aide de parallélogrammes

Construction d'une parallèle en 2 pas

Etant donnés une droite (AB) et un point C extérieur à (AB), on cherche à construire la parallèle à (AB) passant par C, c'est-à-dire un point D tel que (CD) soit parallèle à (AB).

L'idée est de construire un triangle ECD tel que (AB) soit une droite des milieux dans le triangle. Il suffit de construire E, le symétrique de C par rapport à A et D, celui de E par rapport à B. La construction est faite en deux pas.

figure

Droite des mileux

Proposition. Soit un triangle A B C et B' et C' les milieux respectifs des côtés [A C] et [A B].

La droite (B'C'), dite droite des milieux, est parallèle à (BC et on a l'égalité : .

Réciproquement, si une droite passe par C' et est parallèle à (BC) alors elle passe par B' ; c'est la droites de milieux.

Pour dérouler la démonstration de la première affirmation, cliquez sur la flèche..
  1. Soit un triangle ABC et B' et C' les milieux respectifs des côtés [A C] et [A B].
  2. On s'intéresse à la droite des milieux (C'B').
  3. Le point D est le symétrique de C' par rapport à B' donc B' est le milieu de [C'D].
  4. Le quadrilatère A C'C D est un parallélogramme car ses diagonales se coupent en leur milieu.
  5. Comme A C'C D est un parallélogramme, ses cotés [AC'] et [D C] sont parallèles et de même longueur.
  6. Comme C' est le milieu de [A B], on en déduit que les cotés [B C'] et [D C] de B C'D C sont parallèles et de même longueur.
  7. Le quadrilatère convexe B C'D C est donc un parallélogramme.
  8. Les côtés [C'D] et [B C] sont parallèles et de même longueur ; la partie directe de la proposition est démontrée.

Pour démontrer la réciproque, on utilise l'unicité de la parallèle à (B C) passant par C' : si une droite passe par C' et est parallèle à (BC), c'est nécessairement la droite des milieux donc elle passe par B'.

Translation

Définition. Soit un vecteur du plan. On appelle translation de vecteur , notée , la transformation du plan qui à un point M associe le point M' tel que .

Des propriétés du parallélogramme, on déduit la construction de l'image d'un point par une translation donnée. En effet, soient A et B deux points distincts ; le point M' est l'image de M par la translation de vecteur si et seulement si A B M'M est un parallélogramme.

Symétrie orthogonale

Définition : On appelle symétrie orthogonale d'axe et on note la transformation du plan qui à un point M associe le point M' tel que
  1. la droite (M M') est perpendiculaire à .
  2. le milieu I de [M M'] appartient à .
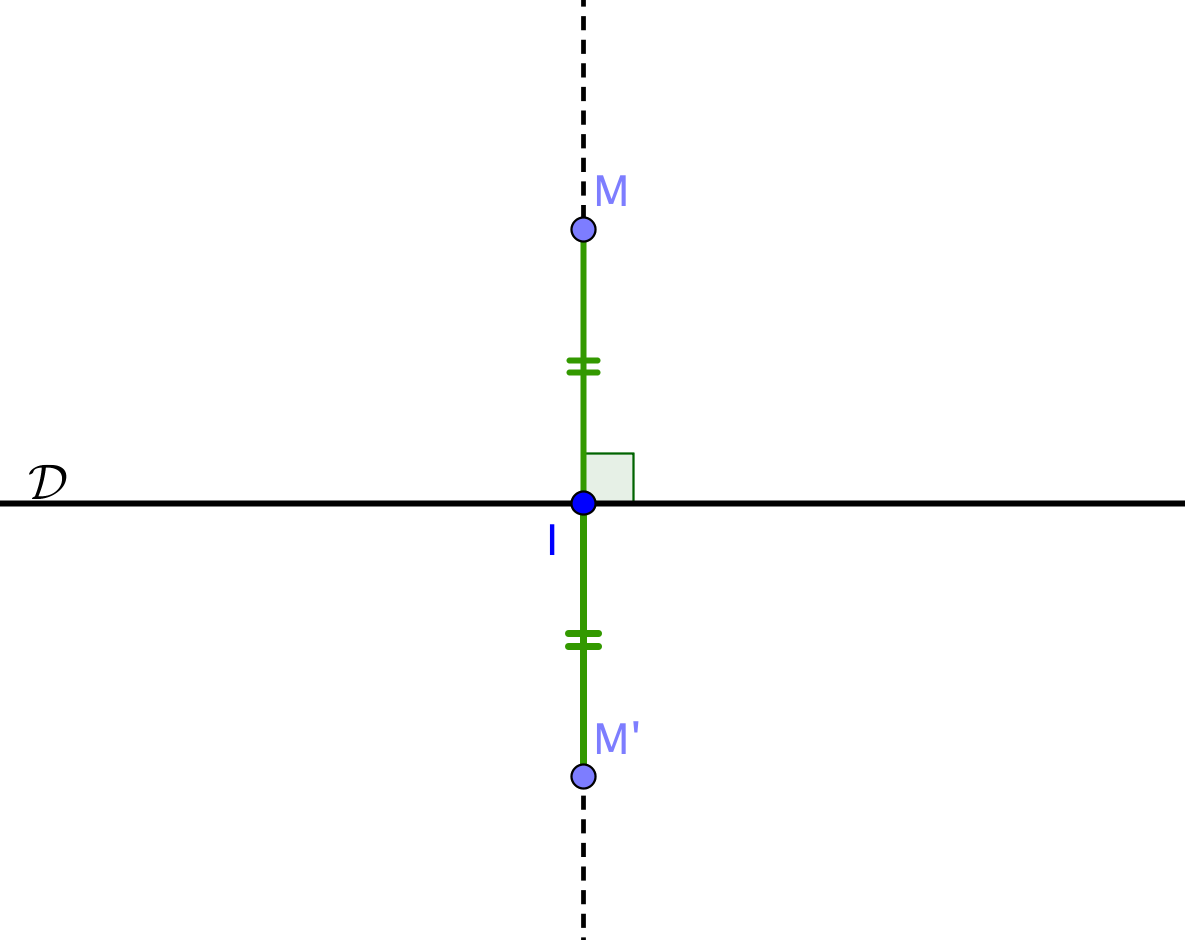
 figure

Propriétés

  1. La symétrie est une isométrie, conserve donc les longueurs et les angles géométriques.
  2. L'axe de est l'ensemble de ses points fixes.
  3. est l'identité, une symétrie est son propre inverse.

Médiatrice d'un segment

Définition : On appelle médiatrice du segment [B C] la droite qui vérifie l'une des propriétés équivalentes suivantes :
  1. est la perpendiculaire à (B C) en A', milieu de [B C].
  2. est l'ensemble des points équidistants des extrémités de [B C].
  3. est l'axe de l'unique réflexion qui échange B et C.

On en déduit le protocole de construction de la médiatrice, du milieu de [B C] et celui d'une perpendiculaire à une droite donnée passant par un point donné .

Proposition : Les médiatrices des côtés d'un triangle sont concourantes en un point O, centre du cercle circonscrit au triangle.

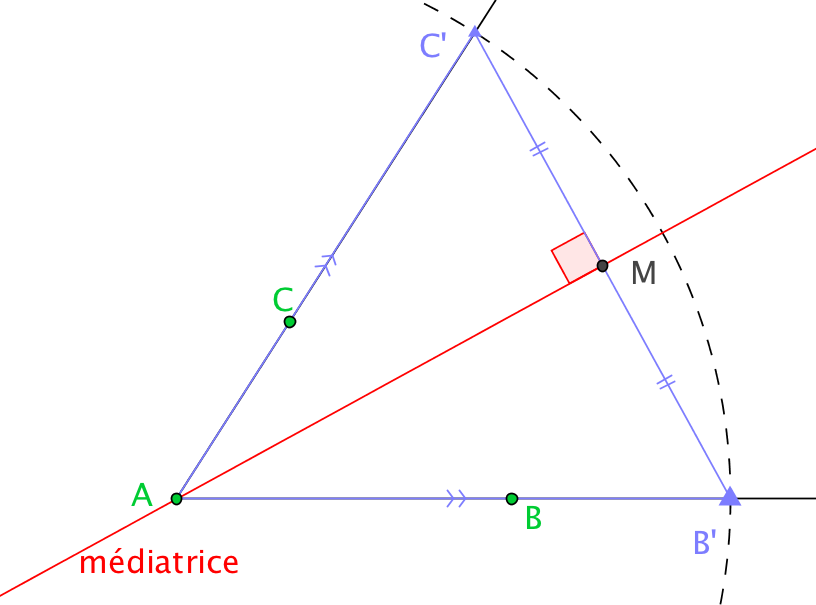
Démonstration. Notons , et les médiatrices respectives de [B C], [C A] et [A B]. Puisque A, B et C ne sont pas alignés, et sont sécantes comme perpendiculaires à deux droites non parallèles. Soit O leur point d'intersection. La caractérisation 2 des médiatrices donne les deux égalités : B O = C O et A O= C O. On en déduit que O est équidistant de A et B donc, toujours par la caractérisation 2 des médiatrices, on obtient que O appartient aussi à . On a démontré que les trois médiatrices sont concourantes en O, point équidistant des trois sommets du triangle, donc centre du cercle passant par les trois sommets du triangle, dit circonscrit au triangle.

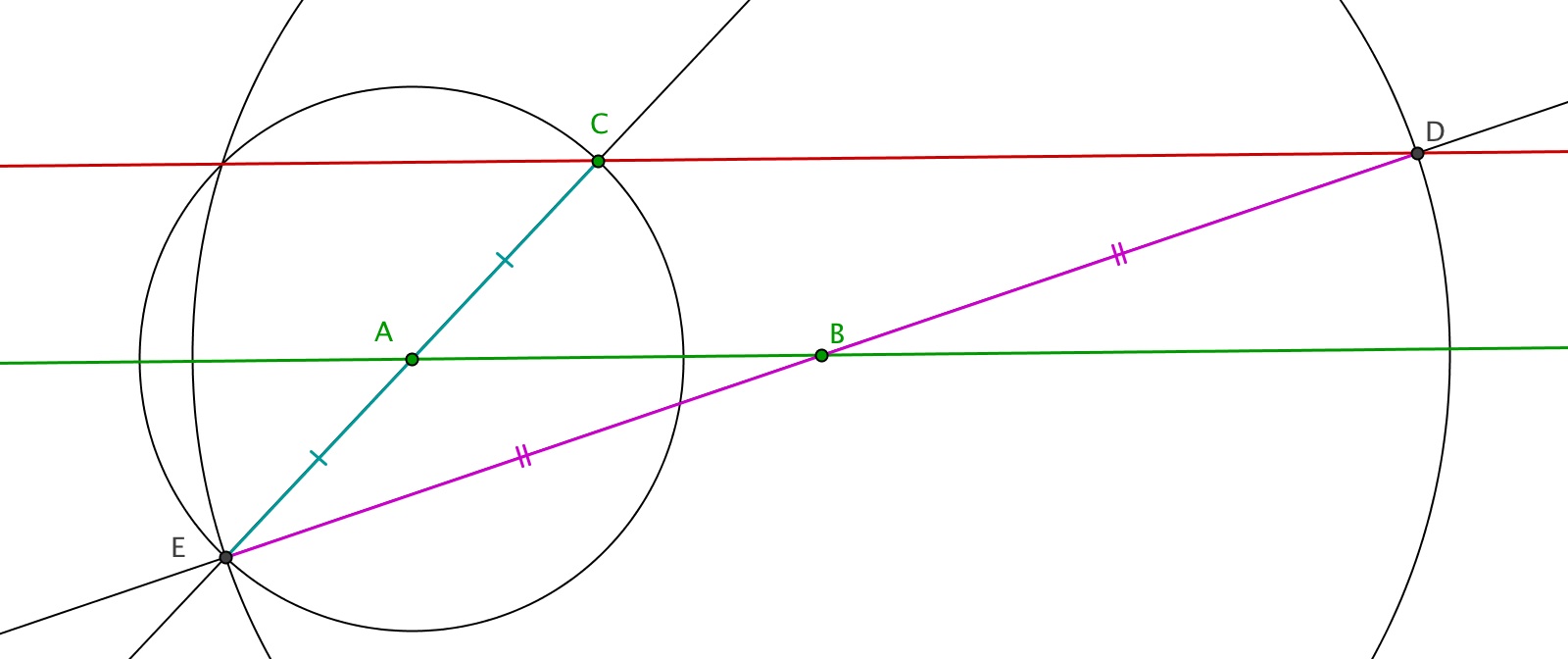
Protocole de construction de la médiatrice et du milieu

Les points donnés sont en vert, les objets construits sont en rouge. La construction de la médiatrice se fait en 2 pas, celle du milieu en 3 pas ( voir [ME VI.1.c]). La médiatrice est la droite (C D) où C et D sont les intersections des cercles et . Le milieu de [A B] est l'intersection de (A B) et (C D).
Déroulez la construction avec les flèches en bas.

Construction d'une perpendiculaire

On cherche à construire la perpendiculaire à (A B) passant par C. Deux cas se présentent :

  1. Soient A, B et C trois points non alignés. Par définition de , la perpendiculaire à (A B) passant par C est la droite (C C') où C' est le symétrique de C par rapport à (A B).
    La construction se fait en un pas : les points C et C' sont les intersections de et . On a utilisé les propriétés 1 et 2 de la symétrie orthogonale et la propriété M2 de la médiatrice .
  2. Soient A, B et C trois points alignés. Soit A' le symétrique de A par rapport à C, alors C est le milieu de [A A'] et la médiatrice de [A A'] est la perpendiculaire à (A B) passant par C. La construction se fait en 3 pas.

Homothétie

Définition. [ME.IV.3.e]
Soit k un réel différent de 0 et de 1 et C un point du plan. On appelle homothétie de centre C et de rapport k (et on note h(C,k)) la transformation du plan qui à un point M associe le point M' tel que .

On peut formuler le théorème de Thalès [ME.IV.1.e] à l'aide d'une homothétie, c'est parfois plus simple, par exemple dans l' espace .

Homothétie et théorème de Thalès

Soit (M M') et (P P') deux droites sécantes en un point C. Il existe une homothétie de centre C qui envoie M sur M' et P sur P' si et seulement si (M P) et (M'P') sont parallèles. Le rapport de l'homothétie est alors :

.

Médianes

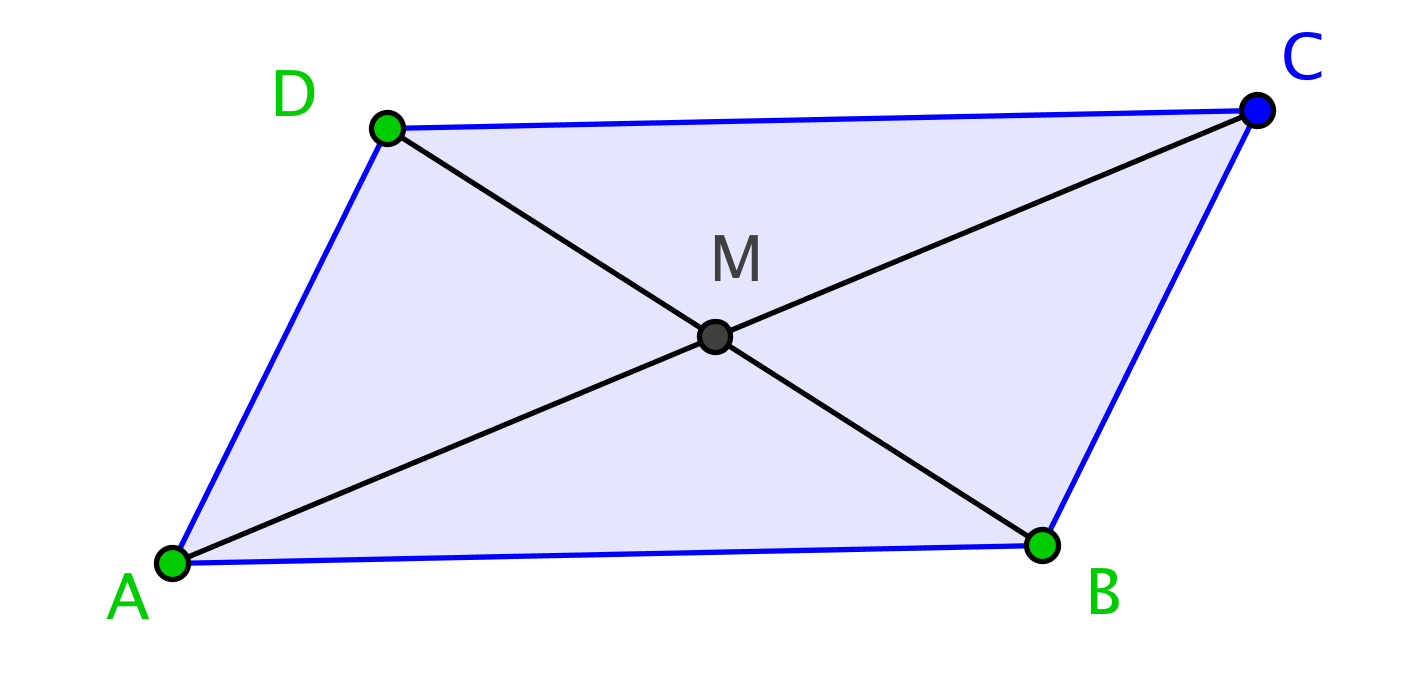
Soit un triangle ABC. On note A', B' et C' les milieux respectifs de [B C], [C A] et [A B].

Définition : On appelle la droite (A A') médiane issue de A dans le triangle A B C.
Proposition : Les médianes de A B C sont concourantes en un point G appelé centre de gravité de A B C. De plus l'homothétie de centre G et de rapport envoie A sur A', B sur B', C sur C'.

Démonstration : On peut démontrer le concours des médianes à l'aide de parallélogrammes , des aires ([ME exercice 194, 192]) ou de l' associativité du barycentre.

Soit G l'isobarycentre de A, B et C. Par associativité, G est le barycentre de puisque A' est le barycentre de . Donc G appartient à la médiane (AA') et on a : et aussi . De même pour les autres médianes.

Remarque : Les triangles ABC et A'B'C' ont même centre de gravité G. En effet, les homothéties conservent les barycentres donc l'image de G est l'isobarycentre de A'B'C'.

On peut voir l'homothétie en action dans une démonstration du concours des hauteurs .

Concours des médianes

Voici une démonstration du concours des médianes d'un triangle qui utilise le théorème de la droite des milieux et les propriétés des parallélogrammes . Les points A', B' et C' sont les milieux respectifs des côtés du triangle ABC.

Pour dérouler la démonstration, cliquez sur la flèche.
  1. Soit un triangle ABC.
  2. Le point G est le point d'intersection des médianes (BB') et (CC').
  3. Soit A'' le symétrique de A par rapport à G.
  4. Dans ABA'', (C'G) est une droite des milieux, donc parallèle à (BA'').
  5. De même, dans ACA'', (B'G) est une droite des milieux, donc parallèle à (CA'').
  6. On en déduit que les côtés opposés de BGCA'' sont parallèles donc c'est un parallélogramme.
  7. Les diagonales de BGCA'' se coupent en leur milieu, donc G appartient à la médiane (AA').

Hauteurs

Définition. Soit A'' le projeté orthogonal de A sur (B C). On appelle hauteur issue de A dans A B C la droite (A A'').

Proposition. Les hauteurs de A B C sont concourantes en un point H appelé orthocentre du triangle A B C.

De nombreuses démonstrations sont possibles pour cette proposition.

Démonstration avec une homothétie

Démonstration avec une homothétie

Le concours des hauteurs se déduit de celui des médiatrices grâce à l'homothétie . En effet l'image de (A A'') par cette homothétie est , car c'est la droite passant par A', image de A, et parallèle à (A A'') donc perpendiculaire à (B C). Les médiatrices sont concourantes en O donc les hauteurs sont concourantes en H=h(G,-2)(O).
Observez la transformation de O en H sur cette autre figure .

Sur la figure, cochez et décochez les deux premières cases pour tester l'homothétie sur les triangles, les deux dernières pour la tester sur la hauteur. Quand le curseur apparaît, vous pouvez faire varier le rapport de l'homothétie.

Relation entre l'orthocentre et le centre du cercle circonscrit

Les hauteurs (en rose) sont envoyées par l'homothétie h(G,k) (quand k atteint -0,5) sur les médiatrices (en bleu). Ainsi h(G,-2) envoie O, le centre du cercle circonscrit au triangle, point de concours de médiatrices sur un point H qui appartient aux 3 hauteurs.

Bissectrice d'un secteur angulaire, d'un angle

Pour la notion de secteur angulaire et d'angle, voir [ME.IV.1.f.].

Bissectrice d'un secteur [ME.IV.1.j.]

Définition et proposition.

Soit un secteur angulaire saillant. Il existe une unique droite passant par A, appelée bissectrice du secteur , telle que les deux demi-droites [A x) et [A y) portées par vérifient :

et

On appelle bissectrice intérieure du secteur celle parmi les demi-droites [A x) et [A y) qui est contenue dans . Dans cette page, on supposera que c'est [A x).

On dit aussi que est la bissectrice de l'angle .

Propriétés de la bissectrice du secteur

  1. La droite est la bissectrice de si et seulement si est axe de symétrie de [A B) et [A C).
  2. Soient et tels que A B' = A C' alors est la bissectrice du secteur si et seulement si est la médiatrice de [B'C'].

Démonstration de la propriété 2 et construction de la bissectrice .

Propriétés de la bissectrice intérieure [A x) du secteur

  1. La demi-droite [A x) partage le secteur en deux secteurs angulaires saillants de même angle.
  2. La demi-droite [A x) est l'ensemble des points de équidistants des demi-droites [A B) et [A C). Démonstration

Construction d'une bissectrice

Propriété 2 de la bissectrice de : Soient et tels que A B' = A C' alors est la bissectrice de si et seulement si est la médiatrice de [B'C'].

Démonstration. : Soit M le point d'intersection de (B'C') et de .

Si est la bissectrice de , on montre à l'aide du premier cas d'isométrie que les triangles B'A M et C'A M sont isométriques. On en déduit que M est le milieu de [B'C'] et que les angles et égaux et supplémentaires sont droits. On a montré que la droite est la médiatrice de [B'C'].

Réciproquement, si est la médiatrice de [B'C'], alors A appartient à et la symétrie d'axe échange B' et C' et fixe A donc elle échange [AB) et [AC), c'est la bissectrice de d'après la propriété 1.

Figure de la partie directeFigure de la réciproque
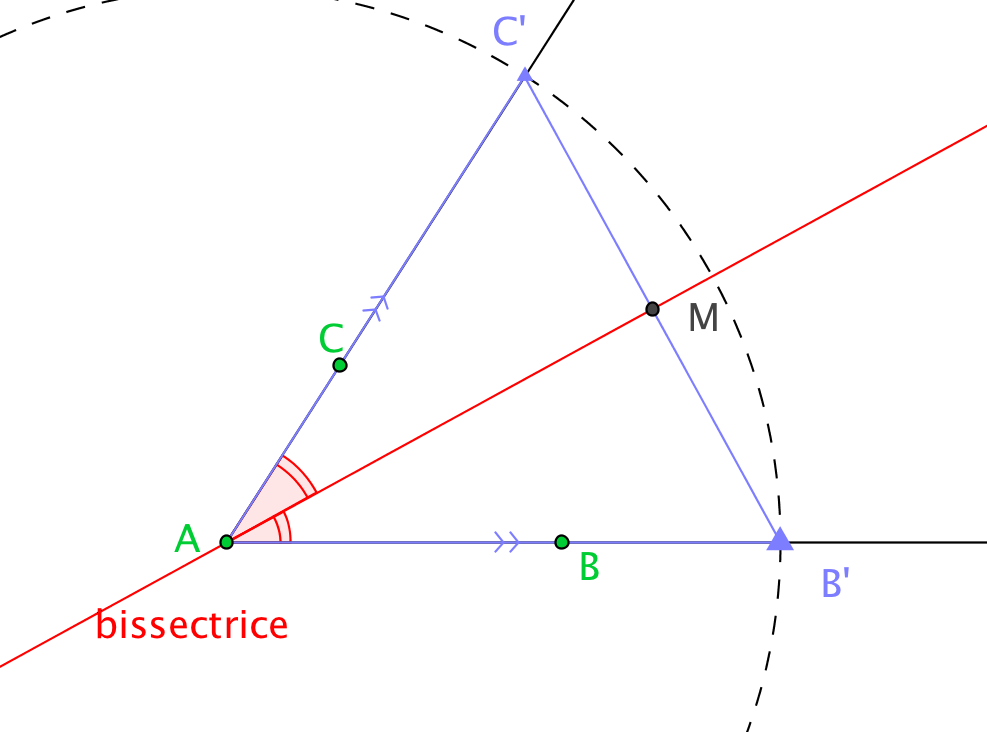figure1figure2

Construction de la bissectrice

On en déduit une construction de la bissectrice [ME. VI.1.g]. Il suffit de construire la médiatrice de deux points équidistants de A, sur la figure, les points B et C'.
Déroulez la construction avec les flèches en bas.


Equidistance et bissectrice

Nous démontrons ici le résultat suivant.
La demi-droite [A x) est l'ensemble des points de équidistants des demi-droites [A B) et [A C).
Pour les deux sens de démonstration, nous considérons les projetés respectifs P et Q de M sur [A B) et [A C) et nous montrons que les triangles A M P et A M Q sont isométriques.
Si M est un point de la bissectrice [A x), alors les angles et sont égaux et les triangles sont isométriques par le deuxième cas ; on en déduit M P = M Q, c'est-à-dire que M est équidistant des demi-droites [A B) et [A C).
Réciproquement si M est équidistant des demi-droites [A B) et [A C), alors les deux triangles rectangles ont deux côtés égaux ( M P = M Q et [A M] commun) donc sont isométriques par le cas des triangles rectangles. Les angles et sont égaux et M appartient à la bissectrice [A x).		 figure1

Bissectrices dans un triangle

Définition. On appellera bissectrice de l'angle en A dans le triangle A B C la bissectrice de l'angle .
Proposition : Soit A B C un triangle. Les bissectrices des angles en A, B et C sont concourantes en un point omega équidistant des côtés du triangle, omega est le centre du cercle inscrit dans ABC. Le cercle inscrit est tangent aux côtés de A B C.

Démonstration. Soit B0 (respectivement C0) le point d'intersection de la bissectrice de l'angle en B (resp. en C) et de [AC] (resp. [AB]). Ces deux bissectrices se coupent en un point , intérieur de A B C, car appartenant à l'intersection des secteurs saillants et . Par la propriété 2 des bissectrices intérieures , est équidistant d'une part de [BA) et de [BC) (sur la figure ), d'autre part de [CA) et [CB) (sur la figure ) donc il est équidistant de [BA) et [CA) (sur la figure ); on en déduit qu'il appartient à la bissectrice de l'angle en A.
Le cercle centré en et passant par les projetés E, F et G de sur les côtés du triangle est tangent à ces côtés donc on le dit inscrit dans le triangle.

Modifiez le triangle pour constater que le cercle reste inscrit.

Triangle isocèle

Définition : On dit que le triangle A B C est isocèle en A si les côtés [A B] et [A C] ont même longueur.
Proposition : Un triangle A B C est isocèle en A si et seulement si ses angles en B et en C sont égaux.

Démonstration. Si les côtés [A B] et [A C] ont même longueur, les triangles A B C et A C B sont isométriques par le 3ème cas . On en déduit l'égalité des angles.
Si les angles en B et en C sont égaux, les triangles A B C et A C B sont isométriques par le 2ème cas . On en déduit l'égalité des côtés.

Proposition : Un triangle A B C est isocèle en A si et seulement si deux des droites remarquables relatives à A sont confondues. Alors elles sont toutes confondues.

Démonstration. On utilise la propriété 2 de la bissectrice et la remarque suivante : Si A appartient à DeltaA, la médiatrice de [B C], alors DeltaA est médiane, hauteur.

Détails de la démonstration

Démonstration

La définition d'un triangle isocèle et la propriété (2) de la médiatrice conduisent au résultat suivant.
Lemme : le triangle A B C est isocèle en A si et seulement A appartient à la médiatrice de [B C].

Soit A B C un triangle tel que l'un des cas suivants se produit (Faites les figures !):

  1. est confondue avec la hauteur ou la médiane ou la bissectrice issue de A.
    Alors A appartient à la médiatrice et, par le lemme, ABC est isocèle.
  2. La hauteur et la médiane issues de A sont confondues . Alors elles sont confondues avec puisque perpendiculaires à [B C] en son milieu. Ce cas se ramène au cas 1.
  3. La hauteur et la bissectrice issues de A sont confondues.
    Si P est le pied de la hauteur, alors les triangles A P B et A P C sont rectangles, avec un côté commun et un autre angle égal donc isométriques par le 2ème cas . On en déduit l'égalité de A B et A C.
  4. La bissectrice et la médiane issues de A sont confondues.
    Soit I le milieu de [B C], H et K ses projetés respectifs sur [A B] et [A C]. Comme I appartient aussi à la bissectrice de , I est équidistant de [A B) et [A C), on a donc I H=I K. Les triangles H I B et K I C sont rectangles, avec deux côtés égaux, ils sont isométriques par le cas des triangles rectangles donc les angles et du triangle A B C sont égaux, A B C est isocèle.

Dans tous les cas, le triangle A B C est isocèle. On a donc montré :

Proposition : Un triangle A B C est isocèle en A si et seulement si deux des droites remarquables relatives à A sont confondues. Alors elles sont toutes confondues.

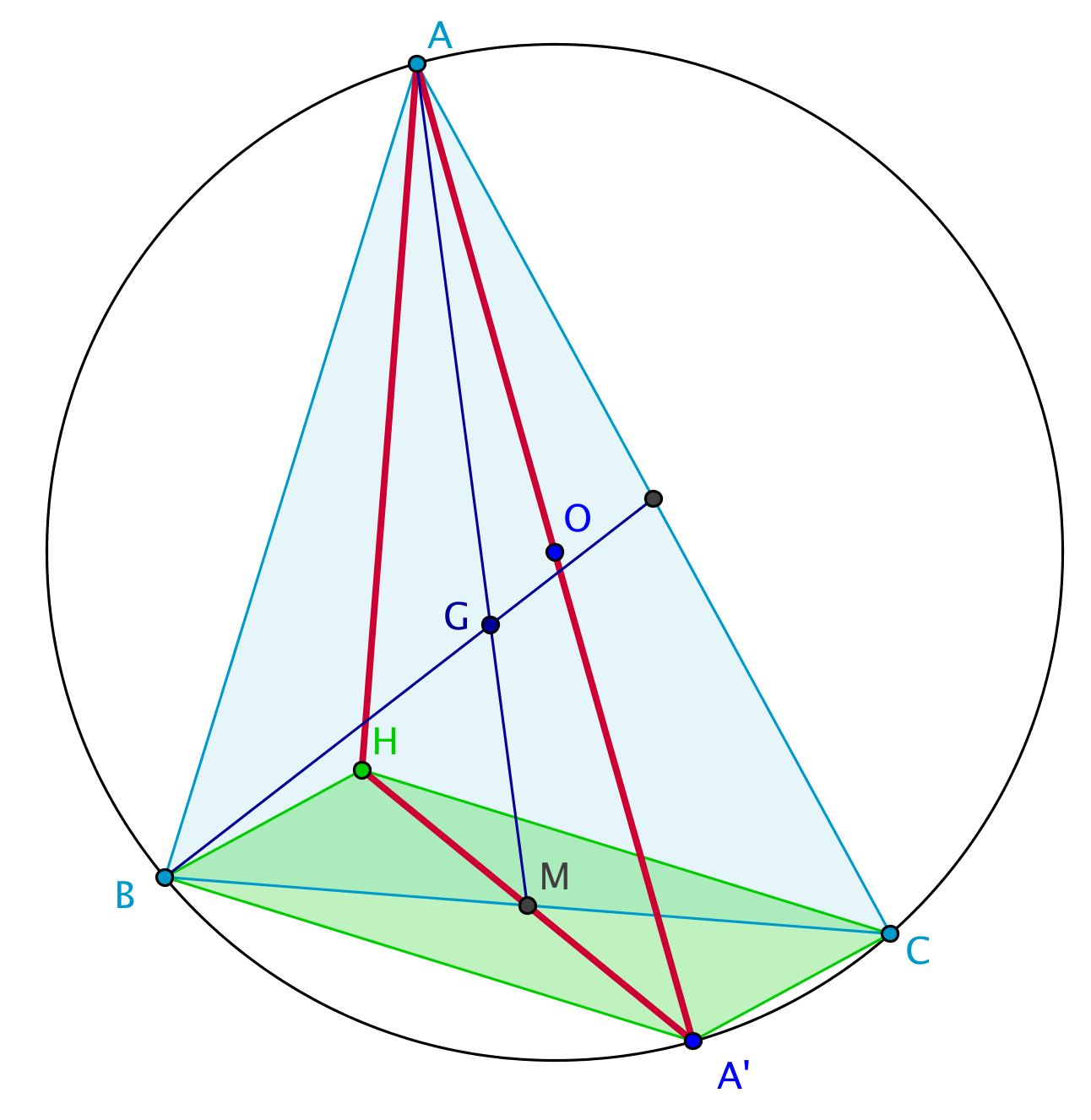
Droite d'Euler

Proposition : S'ils sont différents, les points H, O et G sont alignés sur une droite appelée droite d'Euler du triangle ABC.

Démonstration :

figure Euler au collège

Exercices

Voici quelques exercices sur les droites remarquables.

  1. Reconnaître une droite remarquable sur la figure
  2. Choisir la définition d'une droite remarquable
  3. Donner la définition d'une droite remarquable en lien avec une figure
  4. Tir sur les points de concours des droites remarquables
  5. Définition et position des points de concours des droites remarquables

Vous trouverez d'autres exercices dans la classe ouverte de la licence scientifique générale.

Liste des constructions fondamentales

Les constructions de base présentées dans ce document sont aussi décrites dans [ME.V1.1].

cours : constructions à la règle et au compas, cas d'isométrie ...
: parallelogram, homothétie, translation, symmetry, isometries, triangles, median_line, perpendicular_bisector, altitude, angle_bisector, règle, compas, construction, Euler, interactive mathematics, interactive math, server side interactivity

The most recent version

Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur de web.

Pour accéder aux services de WIMS, vous avez besoin d'un navigateur qui connait les formes. Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

Description: cours : constructions à la règle et au compas, cas d'isométrie ... interactive exercises, online calculators and plotters, mathematical recreation and games

Keywords: interactive mathematics, interactive math, server side interactivity, geometry,, parallelogram, homothétie, translation, symmetry, isometries, triangles, median_line, perpendicular_bisector, altitude, angle_bisector, règle, compas, construction, Euler