Algèbre linéaire : applications linéaires
Objectifs
Guide
Définitions
Définition d'une application linéaire
Définition. Soient
E et
F deux espaces vectoriels sur le même corps K. Une application
f
est une application linéaire si :
- pour tous u et v dans E, f(u+v) = f(u) + f(v) ;
- pour tous
u dans
E et
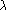 dans K, :
.
dans K, :
.
Cas particuliers.
Soit
f une application linéaire.
- Si F est le corps K, on dit que f est une forme linéaire sur E.
- Si E = F, on dit que f est un endomorphisme de E.
- Si f est bijective, on dit que f est un isomorphisme de E dans (ou sur) F.
- Si f est bijective et E = F, on dit que f est un automorphisme de E.
On note L(E,F) l'ensemble de toutes les applications linéaires de E dans F. Si E = F, on note L(E,F) = L(E).
Propriétés
Proposition Soient
E et
F deux espaces vectoriels sur le corps
K
et
f une
application linéaire. Alors :
-
f(0) = 0 et pour tout
u
 E,
f(-u) = -f(u).
E,
f(-u) = -f(u).
- Pour tous
dans
K
et
u1, u2, ... , un dans
E, on a :
.
- Si G est un sous-espace vectoriel de E, alors f(G) est un sous-espace vectoriel de F.
Proposition(définition
équivalente d'application linéaire) Soient
E et
F deux espaces
vectoriels sur le corps
K. Une application
est une application linéaire si et seulement si
pour tous
u et
v dans
E et 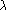
 K,
.
K,
.
Exercice :
Image d'un vecteur par une application linéaire
Exemples
- Pour tout
K-ev
E, les applications
idE et
0E de
E dans
E définies pour
u
 E par :
E par :
idE(u) = u et 0E(u) = 0
sont des applications linéaires de E dans E, donc des endomorphismes de E. On appelle idE l'application identique ou identité de E, idE est un automorphisme de E. On appelle 0E l'application nulle de E (malgré la notation, ne pas confondre avec l'élément neutre de E ), 0E n'est pas un automorphisme de E. - L'application , f((x,y,z)) = -2x + 3y -z, est une forme linéaire sur .
- L'application , f((z1 , z2)) = (z2 , 0) est un endomorphisme de .
- L'application , f((x,y)) = (y,x), est un automorphisme de .
-
Soit
A
 Mp,n(K). L'application
f: Mn,1
Mp,n(K). L'application
f: Mn,1 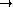 Mp,1, :
, est une application linéaire.
Mp,1, :
, est une application linéaire.
-
L'application
, où
D = Vect((5,4)) (droite vectorielle de
engendrée par le vecteur
(5 , 4)), définie pour
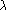

 par
par
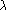 (5,4) est un isomorphisme du
(5,4) est un isomorphisme du  -ev
-ev
 de dimension un sur le sev
D de dimension un du
de dimension un sur le sev
D de dimension un du  -ev
.
-ev
.
Identification
Les isomorphismes nous permettront d'identifier deux espaces vectoriels. Ainsi, on ne peut pas dire que la droite D engendré par le vecteur (1 , 1) (géométriquement, la première bissectrice du plan ) "est" :
D n'est pas un ensemble de nombres,
mais un ensemble de couples. Par contre, "
D est isomorphe à
:
D n'est pas un ensemble de nombres,
mais un ensemble de couples. Par contre, "
D est isomorphe à  " est le langage
qui traduit le fait que, abstraction faite de la nature des éléments de
" est le langage
qui traduit le fait que, abstraction faite de la nature des éléments de
 et de
D,
ces deux espaces vectoriels ont les mêmes propriétés ou le même "comportement".
et de
D,
ces deux espaces vectoriels ont les mêmes propriétés ou le même "comportement".
C'est bien une identification, pas une égalité : on aurait aussi pu considérer la droite comme engendrée par le vecteur (3 , 3) et l'isomorphisme de
 dans
D (c'est-à-dire l'identification de
dans
D (c'est-à-dire l'identification de  avec
D)
aurait alors été l'isomorphisme
avec
D)
aurait alors été l'isomorphisme
et donc un autre isomorphisme.
Noyau et image
- Noyau et image
- Injectivité, surjectivité
- Bases et propriétés d'une application linéaire
- Exemple
- Exercices
Noyau et image
Proposition et définition :
Soient
E et
F deux espaces vectoriels sur le corps
K et
f une application linéaire.
- L'ensemble = est un sous-espace vectoriel de E, appelé le noyau de f.
- L'ensemble est un sous-espace vectoriel de F, appelé l'image de f.
Exercice :
Image réciproque par une application linéaire
Injectivité, surjectivité
Proposition : Soient
E et
F deux espaces vectoriels sur le corps
K et
f une application
linéaire.
- f est injective si et seulement si = .
- f est surjective si et seulement si .
- f est un isomorphisme si et seulement si et .
Proposition et définition :
Soient
E et
F deux espaces vectoriels sur le corps
K et
f
une application linéaire. On suppose que
E est de dimension finie
et que
(a1 , a2, ... , an) est une base de
E. Alors
(f(a1) , f(a2) , ... , f(an)) est une suite génératrice
de
. Par conséquent le sous-espace
est de dimension
finie. On appelle rang de
f, et on note
rang(f), la dimension de
.
Bases et propriétés d'une application linéaire
Lorsque l'espace vectoriel de départ E d'une application linéaire f est de dimension finie, l'on peut "tester" des propriétés de f d'après l'action de f sur les vecteurs d'une base de E, comme le précise la proposition suivante. Proposition : Soient
E et
F deux espaces vectoriels sur le corps
K et
f une
application linéaire. Supposons que
E est de dimension finie
n non nulle et que
(a1 , a2, ... , an) est une base de
E.
- f est injective si et seulement si (f(a1) , f(a2) , ... , f(an)) est une suite libre de F.
- f est surjective si et seulement si (f(a1) , f(a2) , ... , f(an)) engendre F.
- f est un isomorphisme si et seulement si (f(a1) , f(a2) , ... ,f(an)) est une base de F.
Exemple
Exemple : Soient
a 
 et
l'application linéaire
définie pour tout
par
f((x,y,z)) = (2x + y -z , y - z, a z). Soient
b
et
l'application linéaire
définie pour tout
par
f((x,y,z)) = (2x + y -z , y - z, a z). Soient
b 
 et
P le plan vectoriel de
d'équation
x - 2y + b z = 0. On veut déterminer, suivant les valeurs de
a et
b, le sous-espace vectoriel
f(P) de
.
Déterminons une base de
P. Les vecteurs
u = (2 , 1 , 0) et
v = (-b , 0, 1) sont deux vecteurs non colinéaires de
P, donc
(u,v)
est une base de
P. D'après la
proposition,
et
P le plan vectoriel de
d'équation
x - 2y + b z = 0. On veut déterminer, suivant les valeurs de
a et
b, le sous-espace vectoriel
f(P) de
.
Déterminons une base de
P. Les vecteurs
u = (2 , 1 , 0) et
v = (-b , 0, 1) sont deux vecteurs non colinéaires de
P, donc
(u,v)
est une base de
P. D'après la
proposition,

 et
l'application linéaire
définie pour tout
par
f((x,y,z)) = (2x + y -z , y - z, a z). Soient
b
et
l'application linéaire
définie pour tout
par
f((x,y,z)) = (2x + y -z , y - z, a z). Soient
b 
 et
P le plan vectoriel de
d'équation
x - 2y + b z = 0. On veut déterminer, suivant les valeurs de
a et
b, le sous-espace vectoriel
f(P) de
.
Déterminons une base de
P. Les vecteurs
u = (2 , 1 , 0) et
v = (-b , 0, 1) sont deux vecteurs non colinéaires de
P, donc
(u,v)
est une base de
P. D'après la
proposition,
et
P le plan vectoriel de
d'équation
x - 2y + b z = 0. On veut déterminer, suivant les valeurs de
a et
b, le sous-espace vectoriel
f(P) de
.
Déterminons une base de
P. Les vecteurs
u = (2 , 1 , 0) et
v = (-b , 0, 1) sont deux vecteurs non colinéaires de
P, donc
(u,v)
est une base de
P. D'après la
proposition,
L'image d'une base par une application linéaire est une
suite génératrice de l'image de l'application linéaire.
(f(u) , f(v)) est une suite génératrice de
f(P).
Il y a plusieurs cas :
- soit
a est non nul
L'application linéaire f transforme une base de en une base de (car la matrice dont les colonnes sont les vecteurs f(e1), f(e2) et f(e3) est une matrice triangulaire, dont les coefficients diagonaux sont non nuls), d'après la proposition,Si (a1 , ... , an) est une base, f est un isomorphisme si et seulement si (f(a1) , f(a2) , ... , f(an)) est une base de F.f est un automorphisme de et la restriction de f à P est un isomorphisme de P sur f(P) : alors (f(u) , f(v)) est une base de f(P) et f(P) est un plan vectoriel de , pour tout b

 .
.
-
soit
a est nul
L'application linéaire f n'est plus un automorphisme de , mais on ne sait pas a priori si la restriction de f à P est un isomorphisme de P sur f(P). Calculons f(u) = (5 , 1 , 0) et f(v) = (-2b - 1 , -1, 0) ;
- si
b n'est pas égal à 2,
f(u) et f(v) ne sont pas colinéaires, donc (f(u) , f(v)) est une base de f(P), qui est le plan dont une équation cartésienne est z = 0 : f est dans ce cas un isomorphisme de P sur f(P), ce qui découle de la PropositionSi (a1 , ... , an) est une base, f est un isomorphisme si et seulement si (f(a1) , f(a2) , ... , f(an)) est une base de F.ou de la formule
.
- si
b est égal à 2,
f(u) et f(v) sont colinéaires, f(P) est la droite vectorielle de dont une base est (f(u)) ; dans ce cas f n'est pas un isomorphisme de P sur f(P), soit d'après la PropositionSi (a1 , ... , an) est une base, f est un isomorphisme si et seulement si (f(a1) , f(a2) , ... , f(an)) est une base de F.soit d'après l'inclusionKer .
- si
b n'est pas égal à 2,
Exercices
Exercices : ces deux
exercices utilisent la matrice associée à une application linéaire.
- Base de l'image
- Base du noyau
Exercice :
Image et noyau
Exercice :
Image et noyau : application linéaire dépendant d'un paramètre
Matrices
- Matrice et application linéaire
- Exemple générique
- Exemple numérique
- Notation matricielle et systèmes linéaires
- Matrices et composition : le problème
- Produit de matrices
- Exercices sur le produit de matrices
- Matrices et composition : théorème
Matrice et application linéaire
Soient E et F deux espaces de dimension finie. La présence de bases dans E et F va nous permettre d'associer à toute application linéaire de E dans F une matrice.Définition Soient
E et
F deux espaces vectoriels de dimension finie
n  et
p
et
p  , respectivement. Soit
f une application linéaire. Choisissons une base
de
E et
une base
de
F.
On appelle matrice de
f dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
j-ième colonne est constituée par les coordonnées du vecteur
f(aj)
dans la base
, 1
, respectivement. Soit
f une application linéaire. Choisissons une base
de
E et
une base
de
F.
On appelle matrice de
f dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
j-ième colonne est constituée par les coordonnées du vecteur
f(aj)
dans la base
, 1 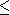 j
j 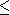 n.
n.
Lorsque
E = F et
, on note
.
La matrice
est une matrice carrée d'ordre
n.
Si on a, pour
:
 et
p
et
p  , respectivement. Soit
f une application linéaire. Choisissons une base
de
E et
une base
de
F.
On appelle matrice de
f dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
j-ième colonne est constituée par les coordonnées du vecteur
f(aj)
dans la base
, 1
, respectivement. Soit
f une application linéaire. Choisissons une base
de
E et
une base
de
F.
On appelle matrice de
f dans les bases
et
la matrice
, notée
(ou parfois
),
dont la
j-ième colonne est constituée par les coordonnées du vecteur
f(aj)
dans la base
, 1 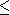 j
j 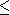 n.
n.
,
c'est-à-dire, si
sont les coordonnées du vecteur
f(uj) dans la base
, alors :
Exemple générique
Prenons n=3 et p=2. Si on aExemple numérique
Prenons n = 3 et p = 2. Si on a
f(u1)=u'1
+
u'2
f(u2)=u'1 + u'2
f(u3)=u'1 + u'2
la matrice de
f dans les bases
et
est f(u2)=u'1 + u'2
f(u3)=u'1 + u'2
[] .
C'est une matrice ayant 2 lignes et 3 colonnes.Exercice :
Matrice associée à une application linéaire
Notation matricielle et systèmes linéaires
Pour tous x = x1 u1 + ... + xn un E et
y = y1 u'1 + ... + yp u'p
E et
y = y1 u'1 + ... + yp u'p  F,
on note
et
les matrices colonnes des
coordonnées des vecteurs
x dans la base
et
y dans la base
, respectivement. Si
, on a alors :
F,
on note
et
les matrices colonnes des
coordonnées des vecteurs
x dans la base
et
y dans la base
, respectivement. Si
, on a alors :
Autrement dit, si A est la matrice de l'application linéaire f dans les bases de E et de F :
résoudre l'équation
f(x) = y
(où
y  F est donné et
x
F est donné et
x  E est l'inconnue)
E est l'inconnue) |
équivaut | résoudre le système linéaire | |
| déterminer le noyau Ker f | équivaut | résoudre le système linéaire homogène ; | on obtient alors une base de Ker f, un système d'équations paramétriques de Ker f et un système d'équations cartésiennes de Ker f |
| déterminer le rang de f, une base et un système d'équations paramétriques de Im f | équivaut | déterminer le rang de la matrice A | c'est-à-dire le rang de la suite des vecteurs colonnes de A |
| déterminer un système d'équations cartésiennes de Im f | équivaut | chercher les conditions de compatibilité du système linéaire |
Matrices et composition : le problème
Question : Soient E, F et G trois K-espaces vectoriels de dimensions finies, munis des bases , et , respectivement. Soient , , . Peut-on calculer C à partir de A et B ? Autrement dit, y a-t-il une opération sur des matrices qui correspond à la composition des applications linéaires qu'elles représentent ?Exemple : Soient
et
dont les matrices,
par rapport aux bases canoniques
de
et
de
sont, respectivement :
Peut-on calculer la matrice à partir des matrices A et B ?
Produit de matrices
Définition Soient
et
.
On appelle produit de la matrice
A par la matrice
B, et on note
AB, la matrice
définie par :
Le produit
A B n'est défini que si le nombre de colonnes de
A est égal
au nombre de lignes de
B. Le produit de deux matrices carrées de même ordre est toujours défini.
Exemple :
| B = | |
| A = | AB = |
Exercices sur le produit de matrices
Exercice :
Trouver deux matrices dont le produit est donné II
Exercice :
Trouver deux matrices dont le produit est donné II
Matrices et composition : théorème
Proposition : Soient
E,
F et
G trois espaces vectoriels sur le corps
K,
de dimension finie
q, n et
p, munis des bases
,
et
respectivement. Si
f  L(E,F) et
g
L(E,F) et
g  L(F,G),
alors :
L(F,G),
alors :
 L(E,F) et
g
L(E,F) et
g  L(F,G),
alors :
L(F,G),
alors :
La situation peut être visualisée :
Corollaire : Soient
p , n , q , r des entiers strictement positifs. Si
A,
A1 et
A2 sont dans
Mp,n(K),
B,
B1 et
B2
sont dans
Mn,q(K),
et
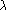
 K, on a :
K, on a :
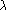
 K, on a :
K, on a :
- A (B C) = (A B) C.
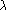 .
.
- A (B1 + B2) = A B1 + A B2.
- (A1 + A2) B = A1 B + A2 B.
Corollaire : Soit
. L'ensemble
Mn(K), muni de l'addition et du
produit de matrices :
est un anneau (non commutatif en général), dont l'élément unité est la matrice identité d'ordre n, notée In.
) et
est un anneau (non commutatif en général), dont l'élément unité est la matrice identité d'ordre n, notée In.
Prolongement par linéarité
Prolongement par linéarité
Comment "fabriquer" des applications linéaires ? Y a-t-il "peu" ou "beaucoup" d'applications linéaires entre deux K-espaces vectoriels ? Nous allons y répondre quand l'espace de départ est de dimension finie. Théorème : Soient
E et
F deux espaces vectoriels sur le corps
K. Supposons que
E est de dimension finie
. Soient
(a1,a2, ... ,an)
une base de
E et
(b1,b2, ... ,bn)
une suite quelconque de vecteurs de
F. Alors il existe une et une
seule application linéaire
f telle que :
f(ai) = bi , 1 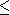 i
i 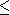 n
n
Corollaire : Soient
E et
F deux
K-espaces vectoriels. Supposons que
E est de dimension finie et qu'il existe un isomorphisme de
E sur
F. Alors
F est de dimension finie,
dim F = dim E et
il existe un isomorphisme de
F dans
E.
Définition :
Deux K-espaces vectoriels
E et
F sont dits
isomorphes s'il existe un isomorphisme de
E sur
F.
C'est le corollaire qui justifie cette définition, lorsque E est de dimension finie ; lorsque ce n'est pas le cas, nous verrons un peu plus tard que l'application réciproque d'un isomorphisme est toujours un isomorphisme.
Corollaire : Soient
E
et
F deux espaces vectoriels de dimension finie
et
p  , respectivement. Soit
f une application linéaire.
Choisissons une base
) de
E
et une base
de
F.
L'application
M
(K) qui
à toute application linéaire
f
, respectivement. Soit
f une application linéaire.
Choisissons une base
) de
E
et une base
de
F.
L'application
M
(K) qui
à toute application linéaire
f  L(E,F) fait correspondre
la matrice
de
f dans les bases
et
est une application bijective.
L(E,F) fait correspondre
la matrice
de
f dans les bases
et
est une application bijective.
 , respectivement. Soit
f une application linéaire.
Choisissons une base
) de
E
et une base
de
F.
L'application
M
(K) qui
à toute application linéaire
f
, respectivement. Soit
f une application linéaire.
Choisissons une base
) de
E
et une base
de
F.
L'application
M
(K) qui
à toute application linéaire
f  L(E,F) fait correspondre
la matrice
de
f dans les bases
et
est une application bijective.
L(E,F) fait correspondre
la matrice
de
f dans les bases
et
est une application bijective.
Exemple de prolongement
Exemple : Soient
u = (1 , -1) et
v = (a , 2) deux vecteurs de
.
Existe-t-il un et un seul endomorphisme
f de
tel que
f(u) = (-2 , 3) et
f(v) = (b ,-6)  ? Si oui, calculer
f(x , y), pour
.
? Si oui, calculer
f(x , y), pour
.
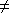 -2.
-2.
 ? Si oui, calculer
f(x , y), pour
.
? Si oui, calculer
f(x , y), pour
.
-
Si a est différent de -2,
(u,v) est une base de et le théorème de prolongement assure l'existence et l'unicité de l'endomorphisme f vérifiant les conditions données. Soit , pour calculer f((x,y)) il suffit d'exprimer (x,y) dans la base (u,v) et utiliser la linéarité de f : , d'où :
= .
-
Si a = -2,
alors v= -2u ; s'il existe un endomorphisme f de vérifiant les conditions données, on a forcément f(v)= -2f(u) ; par conséquent, si , il n'existe pas de tel endomorphisme ; si b =4, il existe une infinité d'endomorphismes f de tels que f(u)=(-2,3) et : soit un vecteur non colinéaire à u, c'est-à-dire, tel que ; (u,w) est une base de et donc, par le théorème de prolongement pour tout , il existe un endomorphisme (unique) de tel que f(u)=(-2,3) et f((a,b))=(c,d).
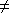 -2.
-2.
Exercice sur le prolongement
Exercice
Existence d'une application linéaire
Le théorème du rang
Théorème du rang
Un théorème important dont la démonstration utilise la notion de supplémentaire est le théorème du rang. Théorème :
Soient
E et
F deux K-espaces vectoriels, avec
E de dimension finie et
f une application linéaire. Alors
Im f est un sous-espace vectoriel de
F de dimension finie et on a :
dim E = dim Ker f + rang f
Corollaire fondamental : Soient
E et
F deux K-espaces vectoriels de même dimension finie
n et
f une application linéaire. Les conditions suivantes sont équivalentes :
- f est un isomorphisme de E sur F.
- f est injective.
- f est surjective.
Exemple d'application du théorème du rang
Application. Le TNI
permet de résoudre certains exercices avec peu de calculs.
Par exemple, soit
l'application linéaire dont la matrice, par rapports aux bases canoniques
de
et
, est
Allons-y.
.
Déterminons Ker f.Allons-y.
La matrice
A, donc
f, a rang 2. D'après le TNI,
dim Ker f = 3 - 2 = 1, donc Ker
f est une droite vectorielle de
. Notons
(e1 , e2 , e3) la base canonique de
,
on "voit" que
,
d'où
est un vecteur non nul de Ker
f, qui est
de dimension 1, donc
u est une base de Ker
f et
.
Changement de bases
- Matrice de changement de bases : définition
- Matrice de changement de bases : propriétés
- Changements de base sur les vecteurs
- Changement de bases sur les matrices
- Exercices sur le changement de base
Matrice de changement de bases : propriétés
Si iE est l'application identique, on a e'j=iE(e'j), , donc P est la matrice de l'application iE dans les bases de E (en tant qu'espace de départ) et de E (en tant qu'espace d'arrivée). Cette interprétation de P est fort importante dans la plupart des raisonnements sur les matrices de changement de base :.
Remarque :
On a
,
la matrice identité d'ordre
n. La matrice
P
est la matrice de
iE lorsqu'on considère dans l'espace de départ
"la nouvelle base"
et dans l'espace d'arrivée "l'ancienne base"
. Donc,
P est la matrice des "nouveaux vecteurs"de base,
par rapport aux "anciens" vecteurs de base.
Proposition : Soient
E un
K-espace vectoriel de dimension finie
,
et
deux bases de
E. La matrice
P  Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
 Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Mn(K)
de passage de la base
à la base
est inversible et
est la matrice de passage de la base
à la base
.
Changements de base sur les vecteurs
Proposition : Soient
E un
K-espace vectoriel de dimension finie
,
et
deux bases de
E et
x  E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
 E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
E. Notons
X et
X' les matrices colonnes des coordonnées du vecteur
x dans les bases
et
, respectivement. Alors :
X = P X' et X' = P-1 X
Exercice :
Changement de bases sur les vecteurs
Changement de bases sur les matrices
Proposition :
Soient
E et
F deux espaces vectoriels de dimensions finies
n et
p, respectivement. Soient
et
deux bases de
E,
et
deux bases de
F,
P  Mn(K) (resp.
Q
Mn(K) (resp.
Q  Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f
Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f  L(E,F),
et
. Alors :
L(E,F),
et
. Alors :
 Mn(K) (resp.
Q
Mn(K) (resp.
Q  Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f
Mp(K))
la matrice de passage de passage de la base
à la base
(resp. de la base
à la base
).
Soient
f  L(E,F),
et
. Alors :
L(E,F),
et
. Alors :
A' = Q-1 A P
Corollaire.
Soient
E un
K-espace vectoriel de dimension finie
n,
et
deux bases de
E. Soient
f  L(E,F),
et
. Soit
P
L(E,F),
et
. Soit
P  Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
 L(E,F),
et
. Soit
P
L(E,F),
et
. Soit
P  Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
Mn(K)
la matrice de passage de passage de la base
à la base
. Alors :
A' = P-1 A P
Exercices sur le changement de base
Exercices :
- Changement de bases
- Matrice d'une application linéaire dans différentes bases
- Changement de base théorique
Matrice de changement de bases : définition
Questions Soient
E et
F deux
K-espaces vectoriels de dimension finie, munis des bases
et
,
respectivement. Comment changent les coordonnées d'un vecteur de
E lorsqu'on change de base dans
E ? Comment change la matrice de
f  L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
 L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
L(E,F) lorsqu'on change de base dans
E et
dans
F ?
Nous allons voir que les changements de base s'expriment par des produits de matrices.
Définition :
Soient
E un
K-espace vectoriel de dimension finie
,
= (u1, u2, ... , un) et
deux bases de
E. La matrice
dont la j-ième colonne est constituée par les coordonnées du vecteur u'j dans la base , , est appelée la matrice de passage de la base à la base . Si on a, pour :
u'j = pj u1 + p2j u2 + ... + pn j un,
c'est-à-dire, si , p2j, ..., pn j sont les coordonnées du vecteur u'j dans la base , alors :