Fonction exponentielle
Introduction
De nombreux phénomènes physiques ou économiques simples
peuvent être modélisés par une fonction
f vérifiant, pour tout réel
x d'un intervalle
I,
où
k est un coefficient réel.
On admet que dans les corps radioactifs, la proportion de noyaux qui se désintègrent pendant une durée de temps est proportionnelle à cette durée. L'évolution du nombre N(t) de noyaux du corps au temps t se modélise alors par la loi suivante, où 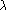 est une constante positive, dépendant seulement du corps radioactif :
est une constante positive, dépendant seulement du corps radioactif :
ce qui équivaut à
pour tout .
Pour de petits intervalles de temps (), on assimile l'expression de gauche au nombre dérivé N'(t). La loi prend la forme d'une équation différentielle, càd une équation qui met en relation la fonction N et sa fonction dérivée N' :
Il est assez facile de montrer que si l'on sait résoudre l'équation différentielle y' = k y avec k = 1, alors on sait résoudre les équations y' = k y avec k quelconque.
Plan
1. Définitions
2. Propriétés algébriques
3. Variations et Limites
4. Exponentielle d'une fonction u : composée exp(u)
5. Logarithme d'un réel strictement positif
6. Equations et inéquations avec exponentielles
7. Primitives
1. Définitions
 telle que
f' = f et
f(0) = 1.
telle que
f' = f et
f(0) = 1.
 .
. et que pour tout réel x on a h'(x) = 0. La fonction h est donc constante. Or pour x = 0, on a h(0) = 1, d'où f(x) f(-x) = 1 quel que soit le réel x.
et que pour tout réel x on a h'(x) = 0. La fonction h est donc constante. Or pour x = 0, on a h(0) = 1, d'où f(x) f(-x) = 1 quel que soit le réel x.
 puisque g ne s'annule pas (cf. Lemme) et dérivable sur
puisque g ne s'annule pas (cf. Lemme) et dérivable sur  comme produit de fonctions dérivables. On montre alors que pour tout réel x. Donc
comme produit de fonctions dérivables. On montre alors que pour tout réel x. Donc  est une fonction constante. Or pour x = 0, on a , d'où f(x) = g(x) quel que soit le réel x.
est une fonction constante. Or pour x = 0, on a , d'où f(x) = g(x) quel que soit le réel x.
Définition :
On appelle fonction exponentielle, et on note exp, l'unique fonction dérivable sur
 solution de l'équation différentielle
y' = y et vérifiant la condition initiale
y(0) = 1.
solution de l'équation différentielle
y' = y et vérifiant la condition initiale
y(0) = 1.
On appelle nombre de Neper, et on note e, l'image de 1 par la fonction exponentielle. On a donc : e = exp(1).
2. Propriétés algébriques
Lemme : Pour tout réel
x on a :
.
On en déduit que la fonction exponentielle ne s'annule pas sur
 .
.
 et que h'(x)=0 pour tout réel x ; on en déduit que la fonction h est constante ; or pour x=0 on a h(0)=1.
et que h'(x)=0 pour tout réel x ; on en déduit que la fonction h est constante ; or pour x=0 on a h(0)=1.Pour tous réels x et y on a :
Pour tout réel x et tout entier relatif n on a : .
Pour un réel y quelconque fixé, on montre que la fonction est dérivable sur
 et que h'(x)=0 pour tout réel x ; on en déduit que la fonction h est constante ; or pour x=0 on a h(0)=1.
et que h'(x)=0 pour tout réel x ; on en déduit que la fonction h est constante ; or pour x=0 on a h(0)=1. La seconde égalité se démontre d'abord par récurrence sur
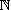 . On la prolonge à
. On la prolonge à  sachant que (cf. Lemme).
sachant que (cf. Lemme).
Notation puissance : La fonction exponentielle prolonge aux réels les règles usuelles des exposants entiers.
Pour tout entier relatif
n on a en effet :
.
Pour tous réels x et y, on a donc les règles suivantes :
 . Sa valeur exacte c'est e !
. Sa valeur exacte c'est e !
Dans un calcul exact, on exprimera donc le résultat en fonction de e.
Pour un calcul approché, on utilisera une approximation : e
 2,7182818...
2,7182818...
Notation puissance
Réécriture sous forme d'une seule exponentielle (1)
Réécriture sous forme d'une seule exponentielle (2)
3. Variations et Limites
Sens de variation et sa fonction dérivée est identique à elle-même.
et sa fonction dérivée est identique à elle-même.
 . Donc, la fonction exponentielle est strictement positive sur
. Donc, la fonction exponentielle est strictement positive sur  .
. . Elle réalise une bijection de
. Elle réalise une bijection de
 sur
.
sur
.
Position relative avec la tangente à l'origine
|
La tangente à la courbe de la fonction exponentielle au point d'abscisse 0 a pour équation .
Propriété : La courbe de la fonction exponentielle est entièrement située
au dessus de sa tangente à l'origine :
|
 atteint un minimum en x = 0. Or la valeur minimale de
atteint un minimum en x = 0. Or la valeur minimale de  est 0. Par suite les valeurs sont toutes positives ou nulles, quel que soit le réel x.
est 0. Par suite les valeurs sont toutes positives ou nulles, quel que soit le réel x.Limites à l'infini
Limite en : On sait que pour tout réel x, . Or donc (théorème de comparaison pour les limites).
Limite en : On sait que pour tout x, . Or , donc par inverse . D'où .
Croissances comparée entre
ex et
xn
En
la fonction exponentielle croît beaucoup plus vite
que les fonctions puissance
.
En l'exponentielle de x est un infini petit qui l'emporte sur toute puissance entière de x.
Exercice :
Choisir des exercices sur les limites.4. Exponentielle d'une fonction u : composée exp(u)
Soit u une fonction définie et dérivable sur un intervalle I.On la note indifféremment ou eu.
C'est à dire, pour tout réel , .
- Si
f est définie sur
 par
, alors pour tout réel
x, on a
.
par
, alors pour tout réel
x, on a
.
-
Exemples (cliquer sur l'icône pour changer les données) :
Soit f la fonction définie sur par
.
par
.
avec . f est dérivable sur et, pour tout réel
x on a :
.
et, pour tout réel
x on a :
.
Exercices :
Calculer la dérivée d'une composée exp(u)
Calculer la limite d'une composée exp(u)
Etude d'une fonction du type \(x \mapsto (a x+b)e^{kx})
Etude d'une fonction du type \(x \mapsto a x+b + e^{kx})
5. Logarithme d'un réel strictement positif
On a vu en 3. que la fonction exponentielle réalise une bijection de sur
. Elle admet donc une bijection réciproque, définie sur
et à valeurs dans
sur
. Elle admet donc une bijection réciproque, définie sur
et à valeurs dans
 .
.
 .
.
On a : et
Propriétés : Les fonctions et étant bijections réciproques l'une de l'autre on a :
- pour tout réel x,
- pour tout réel ,
- pour tout réel x et pour tout réel ,
- les courbes respectives des fonctions exp et ln sont symétriques l'une de l'autre par rapport à la diagonale d'équation
|
|
|
Exercice :
Simplifier une expression6. Equations et inéquations avec exponentielles
Les équations ou inéquations suivantes sont résolvables algébriquement.| Si c > 0, alors | Si c > 0, alors |
| Si , alors l'équation e u = c n'a pas de solution. |
Si
, alors l'inéquation
e u < c n'a pas de solution.
Si , alors l'inéquation e u > c est toujours vraie. |
Exercices :
Résolution guidée d'une inéquation du type \(c*e^{a x+b} > d)
Etude guidée du signe d'une expression du type \((a x+b)*e^{c x+d})
Etude guidée du signe d'une expression du type \(c*e^{a x+b} + d)
En dehors des cas précédents, on ne sait en général pas résoudre une (in)équation avec exponentielle par le calcul algébrique.
On peut parfois, par un changement de variable, se ramener à une équation polynomiale résoluble algébriquement.
Sinon, on utilise une méthode de résolution approchée. En général, on se ramène à résoudre l'équation f(x) = 0. On étudie les variations de la fonction f ; on localise les éventuelles solutions en appliquant le théorème de la bijection dans des intervalles bien choisis ; puis on encadre chaque solution à une précision voulue au moyen de la calculatrice...
7. Primitives
7. Primitives
La fonction admet comme primitives toutes les fonctions où C est une constante réelle, et seulement celles-ci.
Exemples (cliquer sur l'icône pour changer les données) :
Soit
f la fonction définie sur
 par
.
par
.
Alors
f admet comme primitive la fonction
F définie par :
.
Toute autre primitive
G de
f s'écrit :
où
C est une constante réelle.